
Question Number 50420 by Abdo msup. last updated on 16/Dec/18

$${find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:{cosx}\:{ln}\left({cosx}\right){dx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

$${let}\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {cosxln}\left({cosx}\right){dx} \\ $$$$\mid{I}\mid\:{is}\:{the}\:{area}\:{under}\:{the}\:{curve}\:{in}\:{the}\:{given}\:{interval} \\ $$$${area}\:{is}\:{negetive}\:{but}\:{consider}\:{the}\:{value}\:{only}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18
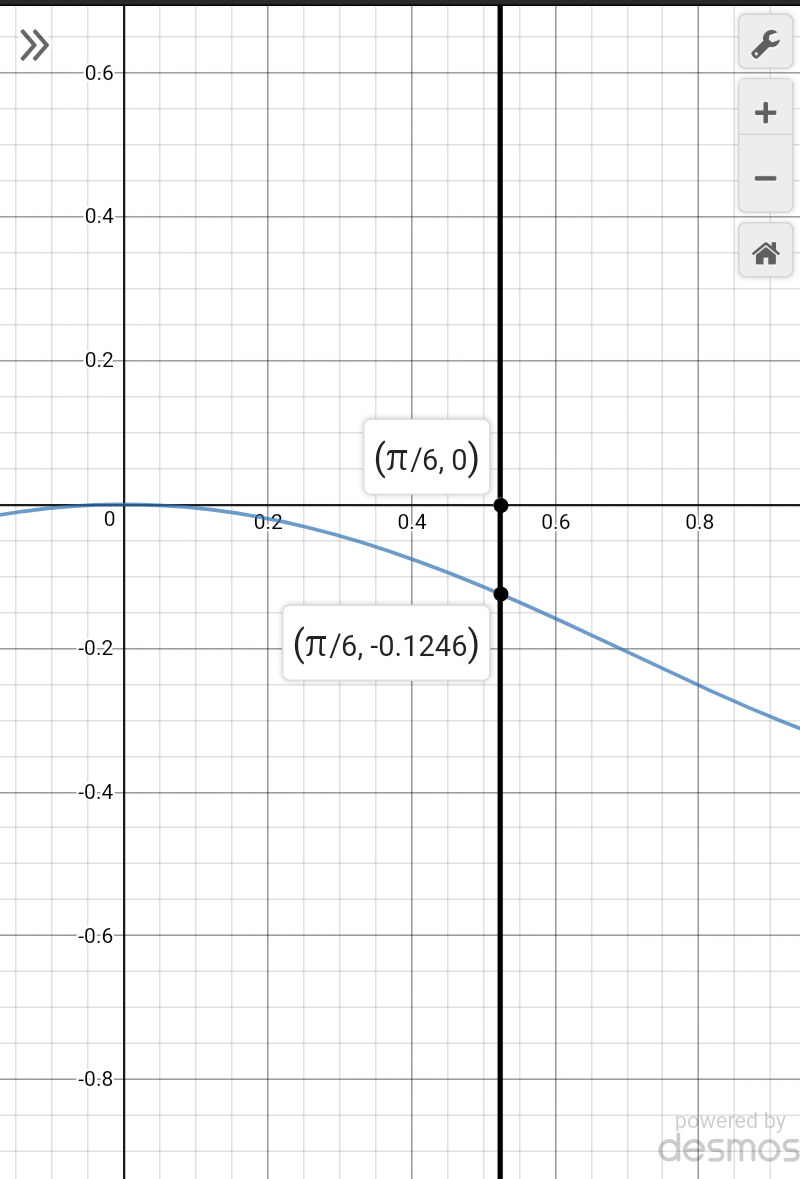
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18
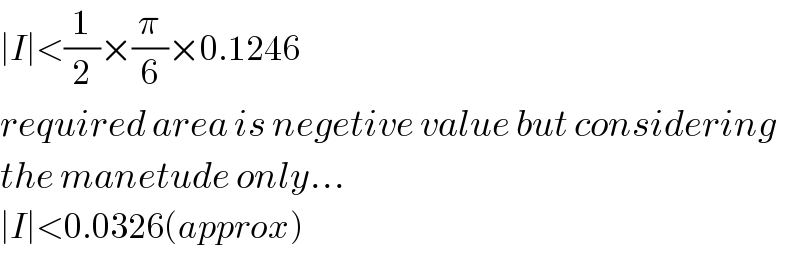
$$\mid{I}\mid<\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{6}}×\mathrm{0}.\mathrm{1246} \\ $$$${required}\:{area}\:{is}\:{negetive}\:{value}\:{but}\:{considering} \\ $$$${the}\:{manetude}\:{only}... \\ $$$$\mid{I}\mid<\mathrm{0}.\mathrm{0326}\left({approx}\right) \\ $$
Commented by maxmathsup by imad last updated on 24/Dec/18
![let A =∫_0 ^(π/6) cosx ln(cosx)dx by parts u^′ =cosx and v=ln(cosx) ⇒ A =[sinx ln(cosx)]_0 ^(π/6) −∫_0 ^(π/6) sinx (−((sinx)/(cosx)))dx =(1/2)ln(((√3)/2)) +∫_0 ^(π/6) ((sin^2 x)/(cosx)) dx but ∫_0 ^(π/6) ((sin^2 x)/(cosx))dx=∫_0 ^(π/6) ((1−cos^2 x)/(cosx))dx =∫_0 ^(π/6) (dx/(cosx)) −∫_0 ^(π/6) cosxdx ∫_0 ^(π/6) cosxdx =[sinx]_0 ^(π/6) =(1/2) ∫_0 ^(π/6) (1/(cosx))dx =_(tan((x/2))=u) ∫_0 ^(tan((π/(12)))) (1/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 )) =∫_0 ^(tan((π/(12)))) ((2du)/((1−u)(1+u))) =∫_0 ^(tan((π/(12)))) ((1/(1−u)) +(1/(1+u)))du = [ln∣((1+u)/(1−u))∣]_0 ^(tan((π/(12)))) =ln∣((1+tan((π/(12))))/(1−tan((π/(12)))))∣ cos^2 ((π/(12)))=((1+cos((π/6)))/2) =((1+((√3)/2))/2) =((2+(√3))/4) ⇒cos((π/(12)))=((√(2+(√3)))/2) we find also sin((π/(12)))=((√(2−(√3)))/2) ⇒tan((π/(12)))=((√(2−(√3)))/(√(2+(√3)))) =((2−(√3))/(√(4−3))) =2−(√3) ⇒ ∫_0 ^(π/6) (dx/(cosx)) =ln∣((3−(√3))/(−1+(√3)))∣ =ln∣(((√3)((√3)−1))/((√3)−1))∣=ln((√3)) ⇒ A =(1/4)ln((3/2))−(1/2) +(1/2)ln(3) =(3/4)ln(3) −(1/4)ln(2)−(1/2) .](Q51133.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{cosx}\:{ln}\left({cosx}\right){dx}\:{by}\:{parts}\:{u}^{'} ={cosx}\:{and}\:{v}={ln}\left({cosx}\right)\:\Rightarrow \\ $$$${A}\:=\left[{sinx}\:{ln}\left({cosx}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{sinx}\:\left(−\frac{{sinx}}{{cosx}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:\frac{{sin}^{\mathrm{2}} {x}}{{cosx}}\:{dx}\:{but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:\frac{{sin}^{\mathrm{2}} {x}}{{cosx}}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{\mathrm{1}−{cos}^{\mathrm{2}} {x}}{{cosx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{{dx}}{{cosx}}\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{cosxdx}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{cosxdx}\:=\left[{sinx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{\mathrm{1}}{{cosx}}{dx}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={u}} \:\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{12}}\right)} \:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{12}}\right)} \:\frac{\mathrm{2}{du}}{\left(\mathrm{1}−{u}\right)\left(\mathrm{1}+{u}\right)} \\ $$$$=\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{12}}\right)} \:\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du}\:=\:\left[{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{12}}\right)} \:={ln}\mid\frac{\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{12}}\right)}{\mathrm{1}−{tan}\left(\frac{\pi}{\mathrm{12}}\right)}\mid \\ $$$${cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)=\frac{\mathrm{1}+{cos}\left(\frac{\pi}{\mathrm{6}}\right)}{\mathrm{2}}\:=\frac{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}}\:=\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{4}}\:\Rightarrow{cos}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$${we}\:{find}\:{also}\:{sin}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\:\Rightarrow{tan}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}\:=\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\sqrt{\mathrm{4}−\mathrm{3}}}\:=\mathrm{2}−\sqrt{\mathrm{3}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:\frac{{dx}}{{cosx}}\:={ln}\mid\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{−\mathrm{1}+\sqrt{\mathrm{3}}}\mid\:={ln}\mid\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\sqrt{\mathrm{3}}−\mathrm{1}}\mid={ln}\left(\sqrt{\mathrm{3}}\right)\:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\:=\frac{\mathrm{3}}{\mathrm{4}}{ln}\left(\mathrm{3}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Answered by Smail last updated on 17/Dec/18
![by parts u=ln(cosx)⇒u′=((−sinx)/(cosx)) v′=cosx⇒v=sinx I=∫_0 ^(π/6) cosxln(cosx)dx =[sinx ln(cosx)]_0 ^(π/6) +∫((sin^2 x)/(cosx))dx =(1/2)ln(((√3)/2))+∫_0 ^(π/6) ((1−cos^2 x)/(cosx))dx =(1/2)ln(((√3)/2))+∫_0 ^(π/6) (dx/(cosx))−∫_0 ^(π/6) cosxdx let t=tan(x/2)⇒dx=((2dt)/(1+t^2 )) I=((ln3)/4)−((ln2)/2)−[sinx]_0 ^(π/6) +2∫_0 ^(tan(π/12)) (dt/(1−t^2 )) I=((ln3)/4)−((ln2)/2)−(1/2)+[ln∣((1+t)/(1−t))∣]_0 ^(tan(π/12)) tan(π/12)=(√((2−(√3))/(2+(√3))))=(√(((2−(√3))^2 )/(4−3)))=2−(√3) I=((ln3)/4)−((ln2)/2)−(1/2)+ln∣((1+2−(√3))/(1−2+(√3)))∣ =((ln3)/4)−((ln2)/2)−(1/2)+ln(3−(√3))−ln((√3)−1)](Q50544.png)
$${by}\:{parts} \\ $$$${u}={ln}\left({cosx}\right)\Rightarrow{u}'=\frac{−{sinx}}{{cosx}} \\ $$$${v}'={cosx}\Rightarrow{v}={sinx} \\ $$$${I}=\int_{\mathrm{0}} ^{\pi/\mathrm{6}} {cosxln}\left({cosx}\right){dx} \\ $$$$=\left[{sinx}\:{ln}\left({cosx}\right)\right]_{\mathrm{0}} ^{\pi/\mathrm{6}} +\int\frac{{sin}^{\mathrm{2}} {x}}{{cosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\int_{\mathrm{0}} ^{\pi/\mathrm{6}} \frac{\mathrm{1}−{cos}^{\mathrm{2}} {x}}{{cosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\int_{\mathrm{0}} ^{\pi/\mathrm{6}} \frac{{dx}}{{cosx}}−\int_{\mathrm{0}} ^{\pi/\mathrm{6}} {cosxdx} \\ $$$${let}\:{t}={tan}\left({x}/\mathrm{2}\right)\Rightarrow{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}=\frac{{ln}\mathrm{3}}{\mathrm{4}}−\frac{{ln}\mathrm{2}}{\mathrm{2}}−\left[{sinx}\right]_{\mathrm{0}} ^{\pi/\mathrm{6}} +\mathrm{2}\int_{\mathrm{0}} ^{{tan}\left(\pi/\mathrm{12}\right)} \frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$${I}=\frac{{ln}\mathrm{3}}{\mathrm{4}}−\frac{{ln}\mathrm{2}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}+\left[{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\right]_{\mathrm{0}} ^{{tan}\left(\pi/\mathrm{12}\right)} \\ $$$${tan}\left(\pi/\mathrm{12}\right)=\sqrt{\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}}}=\sqrt{\frac{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{4}−\mathrm{3}}}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${I}=\frac{{ln}\mathrm{3}}{\mathrm{4}}−\frac{{ln}\mathrm{2}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}+{ln}\mid\frac{\mathrm{1}+\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{1}−\mathrm{2}+\sqrt{\mathrm{3}}}\mid \\ $$$$=\frac{{ln}\mathrm{3}}{\mathrm{4}}−\frac{{ln}\mathrm{2}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}+{ln}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)−{ln}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 17/Dec/18
$${thank}\:{you}\:{sir}\:{smail}. \\ $$
