
Question Number 115361 by Bird last updated on 25/Sep/20
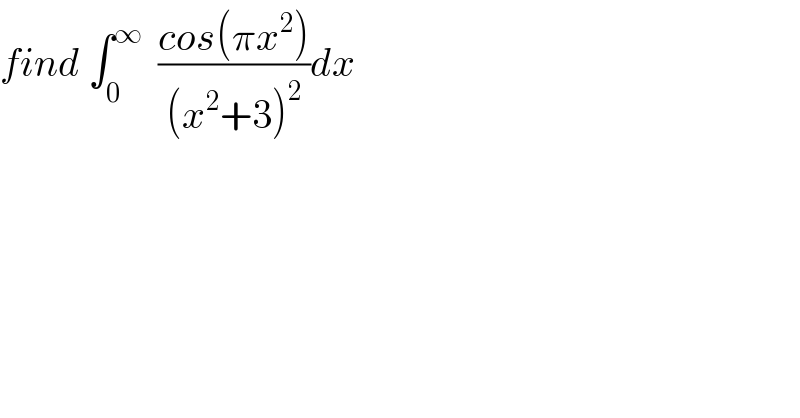
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left(\pi{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by Olaf last updated on 27/Sep/20
![((π[6π(C((√6))−S((√6)))+C((√6))−S((√6))+(√6)−1])/(12(√3))) ≈ 0.0422927](Q115609.png)
$$\frac{\pi\left[\mathrm{6}\pi\left(\boldsymbol{\mathrm{C}}\left(\sqrt{\mathrm{6}}\right)−\boldsymbol{\mathrm{S}}\left(\sqrt{\mathrm{6}}\right)\right)+\boldsymbol{\mathrm{C}}\left(\sqrt{\mathrm{6}}\right)−\boldsymbol{\mathrm{S}}\left(\sqrt{\mathrm{6}}\right)+\sqrt{\mathrm{6}}−\mathrm{1}\right]}{\mathrm{12}\sqrt{\mathrm{3}}} \\ $$$$\approx\:\mathrm{0}.\mathrm{0422927} \\ $$
