
Question Number 114395 by mathmax by abdo last updated on 18/Sep/20
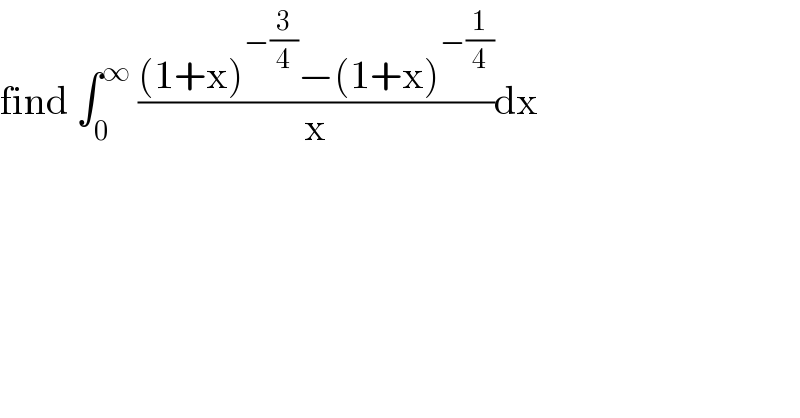
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{1}+\mathrm{x}\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} −\left(\mathrm{1}+\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{x}}\mathrm{dx} \\ $$
Answered by Olaf last updated on 19/Sep/20
![I = ∫_0 ^∞ (((1+x)^(−(3/4)) −(1+x)^(−(1/4)) )/x)dx u = (1+x)^(1/4) du = (1/4)(1+x)^(−(3/4)) dx = (dx/(4u^3 )) I = ∫_1 ^∞ (((1/u^3 )−(1/u))/(u^4 −1)).4u^3 du I = 4∫_1 ^∞ ((1−u^2 )/(u^4 −1))du I = −4∫_1 ^∞ (du/(1+u^2 )) I = −4[arctanu]_1 ^∞ = −4((π/2)−(π/4)) = −π](Q114404.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{1}+{x}\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} −\left(\mathrm{1}+{x}\right)^{−\frac{\mathrm{1}}{\mathrm{4}}} }{{x}}{dx} \\ $$$${u}\:=\:\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${du}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+{x}\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} {dx}\:=\:\frac{{dx}}{\mathrm{4}{u}^{\mathrm{3}} } \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{1}} ^{\infty} \frac{\frac{\mathrm{1}}{{u}^{\mathrm{3}} }−\frac{\mathrm{1}}{{u}}}{{u}^{\mathrm{4}} −\mathrm{1}}.\mathrm{4}{u}^{\mathrm{3}} {du} \\ $$$$\mathrm{I}\:=\:\mathrm{4}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}−{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} −\mathrm{1}}{du} \\ $$$$\mathrm{I}\:=\:−\mathrm{4}\int_{\mathrm{1}} ^{\infty} \frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:−\mathrm{4}\left[\mathrm{arctan}{u}\right]_{\mathrm{1}} ^{\infty} \:=\:−\mathrm{4}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)\:=\:−\pi \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
