
Question Number 42803 by maxmathsup by imad last updated on 02/Sep/18
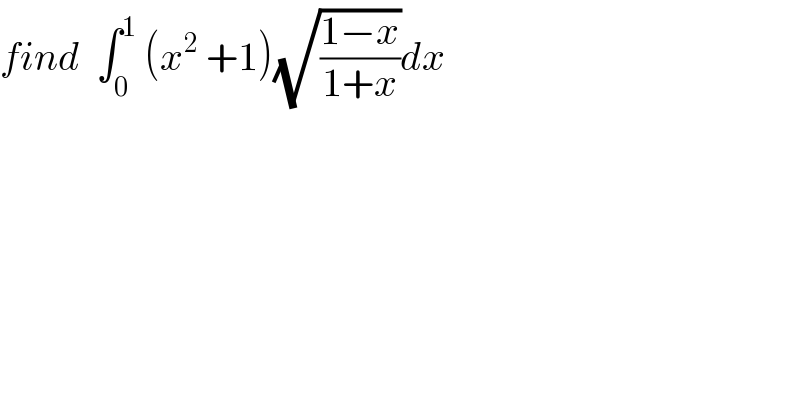
$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{dx}\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Sep/18
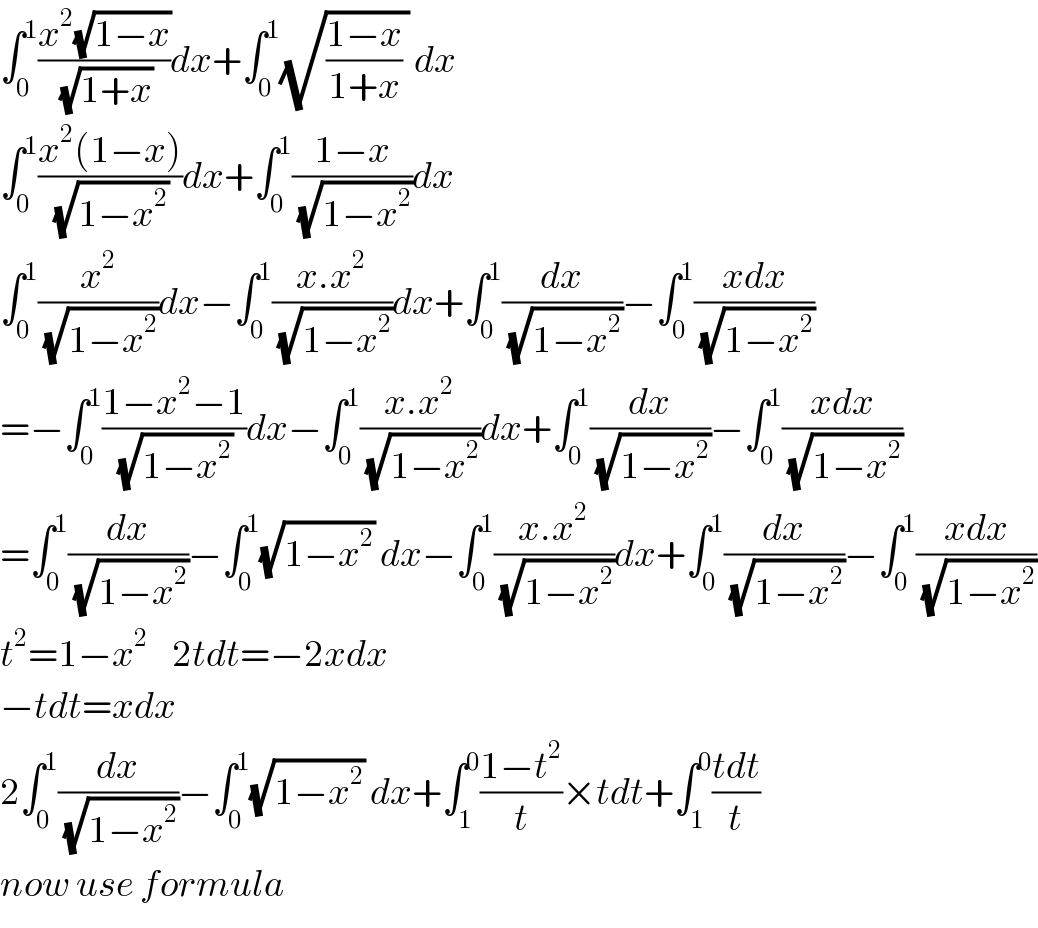
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}}}{\sqrt{\mathrm{1}+{x}}}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:}\:{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}.{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xdx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{2}} −\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}.{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xdx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}.{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xdx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${t}^{\mathrm{2}} =\mathrm{1}−{x}^{\mathrm{2}} \:\:\:\:\mathrm{2}{tdt}=−\mathrm{2}{xdx} \\ $$$$−{tdt}={xdx} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}+\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}}×{tdt}+\int_{\mathrm{1}} ^{\mathrm{0}} \frac{{tdt}}{{t}} \\ $$$${now}\:{use}\:{formula} \\ $$
