
Question Number 112446 by mathmax by abdo last updated on 07/Sep/20
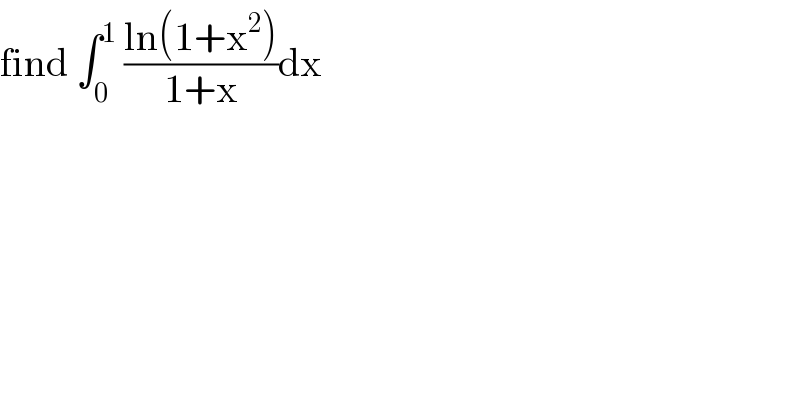
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$
Answered by mathdave last updated on 08/Sep/20
)/x)dx I_1 =∫_0 ^1 ((ln(1+x))/x)dx−∫_0 ^1 ((ln(1+x))/(x(1+x^2 )))dx adopt faynmann trick I_1 =∫_0 ^1 ((ln(1+x))/x)dx−∫_0 ^1 (1/(1+x^2 ))(∫_0 ^1 (1/(1+xy))dy)dx I_1 =η(2)−∫_0 ^1 (1/(1+y^2 ))∫_0 ^1 [(y^2 /(1+xy))+((1−xy)/(1+x^2 ))]dxdy I_1 =(π^2 /(12))−∫_0 ^1 (1/(1+y^2 ))[yln(1+y)+(π/4)−(y/2)ln2]dy I_1 =(π^2 /(12))−∫_0 ^1 ((yln(1+y))/(1+y^2 ))−(π/4)∫_0 ^1 (1/(1+y^2 ))dy+(1/2)ln2∫_0 ^1 (y/(1+y^2 ))dy I_1 =(π^2 /(12))−I_1 −(π^2 /(16))+((ln^2 (2))/4) 2I_1 =(π^2 /(48))+((ln^2 (2))/4) ∵I_1 =(π^2 /(96))+((ln^2 (2))/8) recall that I=ln^2 (2)−2I_1 .........(1) ∵I=ln^2 (2)−2[(π^2 /(96))+((ln^2 (2))/8)] I=ln^2 (2)−((.π^2 )/(48))−((ln^2 (2))/4) I=(3/4)ln^2 (2)−(π^2 /(48)) ∵∫_0 ^1 ((ln(1+x^2 ))/(1+x))dx=(3/4)ln^2 (2)−(π^2 /(48)) by mathdave(08/09/2020)](Q112484.png)
$${solution}\:{to}\: \\ $$$${let}\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}}{dx}\:\:\:{using}\:{IBP} \\ $$$${I}=\mid\mathrm{ln}\left(\mathrm{1}+{x}\right)\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${I}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{2}{I}_{\mathrm{1}} ........\left(\mathrm{1}\right) \\ $$$${Let}\: \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left[\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\right]\frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$${adopt}\:{faynmann}\:{trick} \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{xy}}{dy}\right){dx} \\ $$$${I}_{\mathrm{1}} =\eta\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \left[\frac{{y}^{\mathrm{2}} }{\mathrm{1}+{xy}}+\frac{\mathrm{1}−{xy}}{\mathrm{1}+{x}^{\mathrm{2}} }\right]{dxdy} \\ $$$${I}_{\mathrm{1}} =\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} }\left[{y}\mathrm{ln}\left(\mathrm{1}+{y}\right)+\frac{\pi}{\mathrm{4}}−\frac{{y}}{\mathrm{2}}\mathrm{ln2}\right]{dy} \\ $$$${I}_{\mathrm{1}} =\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{y}\mathrm{ln}\left(\mathrm{1}+{y}\right)}{\mathrm{1}+{y}^{\mathrm{2}} }−\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} }{dy}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{y}}{\mathrm{1}+{y}^{\mathrm{2}} }{dy} \\ $$$${I}_{\mathrm{1}} =\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−{I}_{\mathrm{1}} −\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\mathrm{2}{I}_{\mathrm{1}} =\frac{\pi^{\mathrm{2}} }{\mathrm{48}}+\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\because{I}_{\mathrm{1}} =\frac{\pi^{\mathrm{2}} }{\mathrm{96}}+\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$${recall}\:{that}\:\:\:{I}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{2}{I}_{\mathrm{1}} .........\left(\mathrm{1}\right) \\ $$$$\because{I}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{2}\left[\frac{\pi^{\mathrm{2}} }{\mathrm{96}}+\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{8}}\right] \\ $$$${I}=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{.\pi^{\mathrm{2}} }{\mathrm{48}}−\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$${I}=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{48}} \\ $$$$\because\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}}{dx}=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{48}} \\ $$$${by}\:{mathdave}\left(\mathrm{08}/\mathrm{09}/\mathrm{2020}\right) \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 08/Sep/20

$$\mathrm{thanks} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by mnjuly1970 last updated on 08/Sep/20
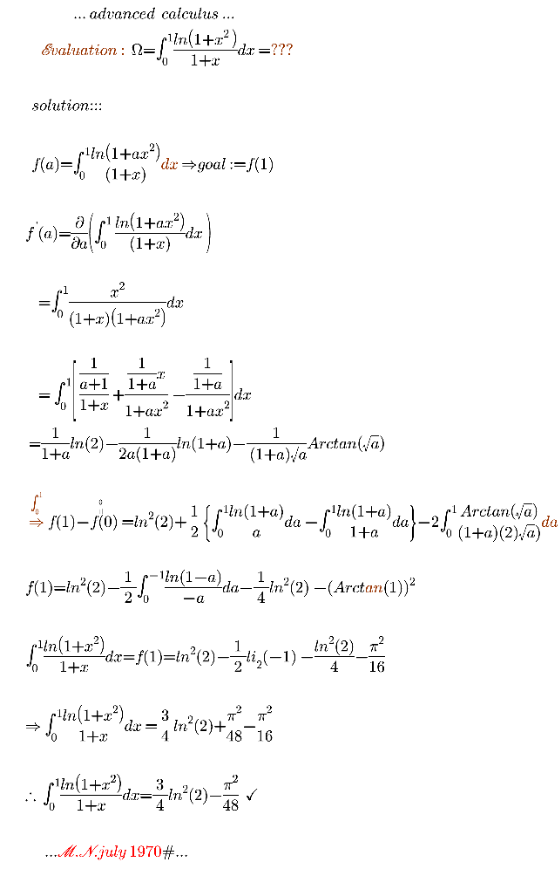
Commented by mathmax by abdo last updated on 08/Sep/20

$$\mathrm{thanks} \\ $$
Commented by mnjuly1970 last updated on 08/Sep/20
$${grateful}\:{sir}\:.{to}\:{me}\: \\ $$$${you}\:{are}\:'{ostad}'\left(\:{in}\:{our}\right. \\ $$$${language}\:{means}\:\:'{master} \\ $$$$\left.{and}\:{scholar}'\:{in}\:{his}\:{field}\right) \\ $$$${in}\:{mathematics}\:.\:{thank} \\ $$$${you}\:{so}\:{much}\:{sir}\:{for}\:{your} \\ $$$${effort}\:.... \\ $$
