
Question Number 124321 by sogol last updated on 02/Dec/20
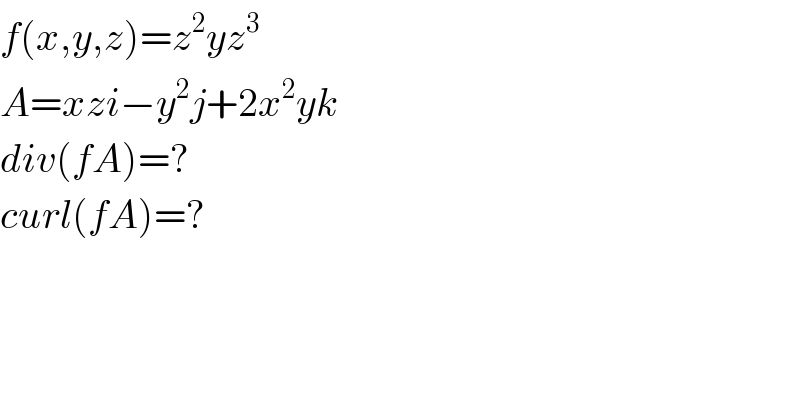
$${f}\left({x},{y},{z}\right)={z}^{\mathrm{2}} {yz}^{\mathrm{3}} \\ $$$${A}={xzi}−{y}^{\mathrm{2}} {j}+\mathrm{2}{x}^{\mathrm{2}} {yk} \\ $$$${div}\left({fA}\right)=? \\ $$$${curl}\left({fA}\right)=? \\ $$
Answered by Ar Brandon last updated on 02/Dec/20
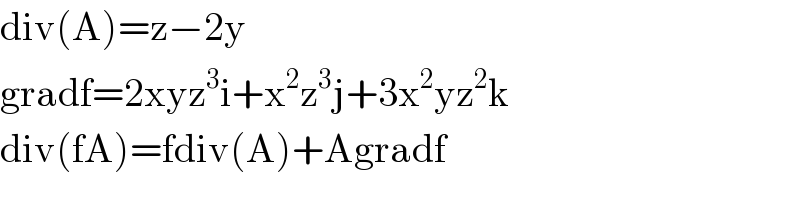
$$\mathrm{div}\left(\mathrm{A}\right)=\mathrm{z}−\mathrm{2y} \\ $$$$\mathrm{gradf}=\mathrm{2xyz}^{\mathrm{3}} \mathrm{i}+\mathrm{x}^{\mathrm{2}} \mathrm{z}^{\mathrm{3}} \mathrm{j}+\mathrm{3x}^{\mathrm{2}} \mathrm{yz}^{\mathrm{2}} \mathrm{k} \\ $$$$\mathrm{div}\left(\mathrm{fA}\right)=\mathrm{fdiv}\left(\mathrm{A}\right)+\mathrm{Agradf} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Dec/20
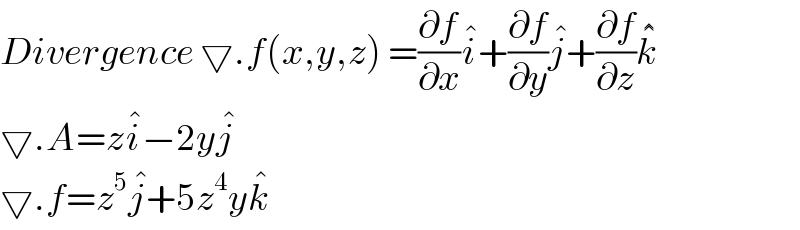
$${Divergence}\:\bigtriangledown.{f}\left({x},{y},{z}\right)\:=\frac{\partial{f}}{\partial{x}}\hat {{i}}+\frac{\partial{f}}{\partial{y}}\hat {{j}}+\frac{\partial{f}}{\partial{z}}\hat {{k}} \\ $$$$\bigtriangledown.{A}={z}\hat {{i}}−\mathrm{2}{y}\hat {{j}} \\ $$$$\bigtriangledown.{f}={z}^{\mathrm{5}} \hat {{j}}+\mathrm{5}{z}^{\mathrm{4}} {y}\hat {{k}} \\ $$
