
Question Number 923 by 123456 last updated on 25/Apr/15
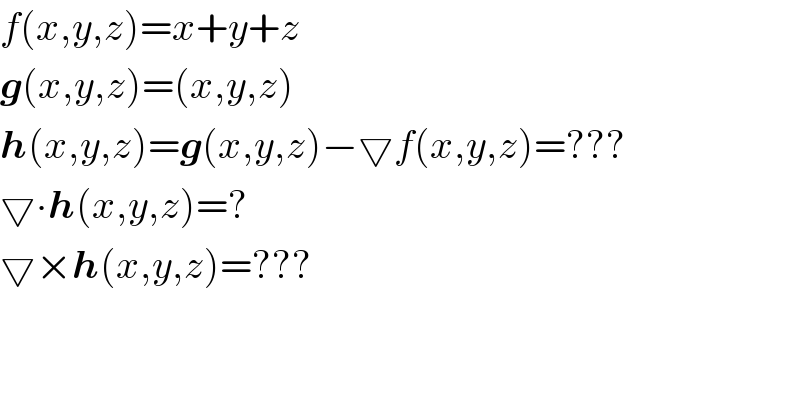
$${f}\left({x},{y},{z}\right)={x}+{y}+{z} \\ $$$$\boldsymbol{{g}}\left({x},{y},{z}\right)=\left({x},{y},{z}\right) \\ $$$$\boldsymbol{{h}}\left({x},{y},{z}\right)=\boldsymbol{{g}}\left({x},{y},{z}\right)−\bigtriangledown{f}\left({x},{y},{z}\right)=??? \\ $$$$\bigtriangledown\centerdot\boldsymbol{{h}}\left({x},{y},{z}\right)=? \\ $$$$\bigtriangledown×\boldsymbol{{h}}\left({x},{y},{z}\right)=??? \\ $$
Answered by 2closedStringsMeet last updated on 15/Aug/15
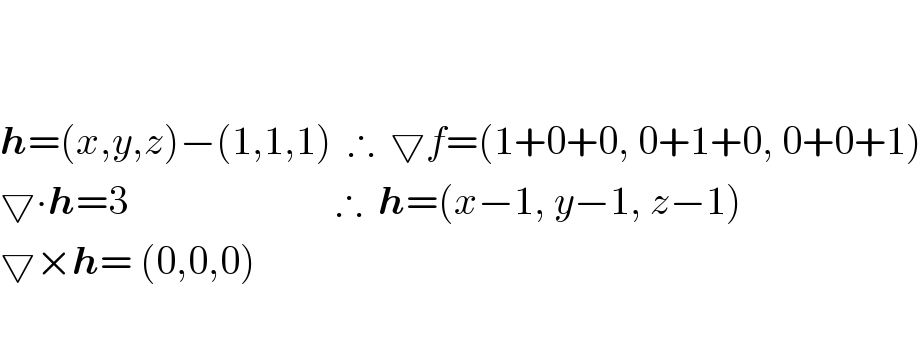
$$ \\ $$$$ \\ $$$$\boldsymbol{{h}}=\left({x},{y},{z}\right)−\left(\mathrm{1},\mathrm{1},\mathrm{1}\right)\:\:\therefore\:\:\bigtriangledown{f}=\left(\mathrm{1}+\mathrm{0}+\mathrm{0},\:\mathrm{0}+\mathrm{1}+\mathrm{0},\:\mathrm{0}+\mathrm{0}+\mathrm{1}\right) \\ $$$$\bigtriangledown\centerdot\boldsymbol{{h}}=\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\boldsymbol{{h}}=\left({x}−\mathrm{1},\:{y}−\mathrm{1},\:{z}−\mathrm{1}\right) \\ $$$$\bigtriangledown×\boldsymbol{{h}}=\:\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$ \\ $$
