
Question Number 168979 by MikeH last updated on 22/Apr/22
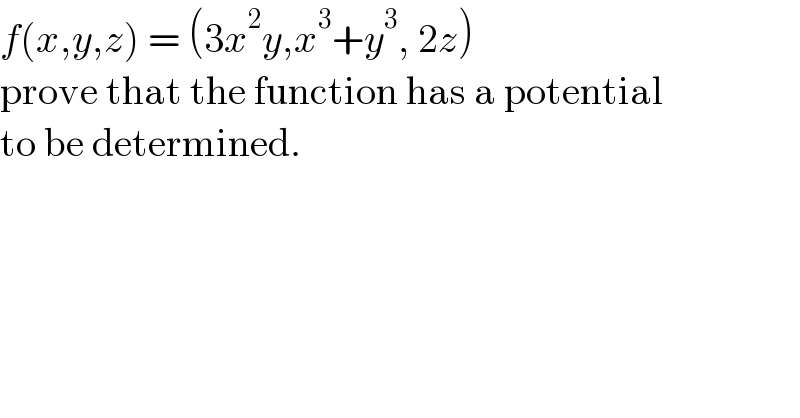
$${f}\left({x},{y},{z}\right)\:=\:\left(\mathrm{3}{x}^{\mathrm{2}} {y},{x}^{\mathrm{3}} +{y}^{\mathrm{3}} ,\:\mathrm{2}{z}\right) \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{function}\:\mathrm{has}\:\mathrm{a}\:\mathrm{potential} \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{determined}. \\ $$
