
Previous in Relation and Functions Next in Relation and Functions
Question Number 1842 by 123456 last updated on 12/Oct/15
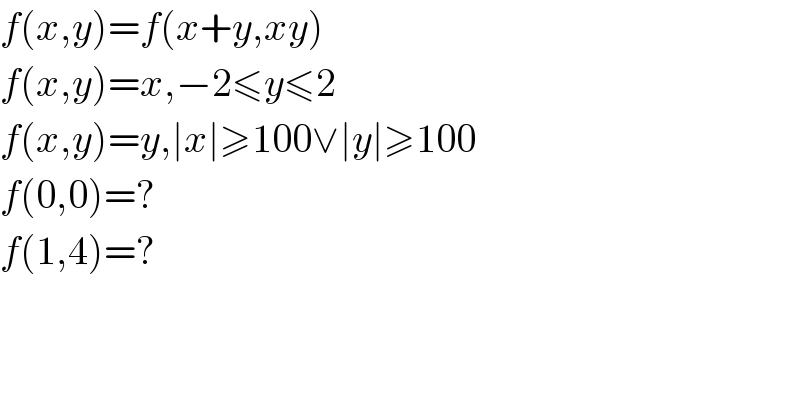
$${f}\left({x},{y}\right)={f}\left({x}+{y},{xy}\right) \\ $$$${f}\left({x},{y}\right)={x},−\mathrm{2}\leqslant{y}\leqslant\mathrm{2} \\ $$$${f}\left({x},{y}\right)={y},\mid{x}\mid\geqslant\mathrm{100}\vee\mid{y}\mid\geqslant\mathrm{100} \\ $$$${f}\left(\mathrm{0},\mathrm{0}\right)=? \\ $$$${f}\left(\mathrm{1},\mathrm{4}\right)=? \\ $$
Commented by 123456 last updated on 12/Oct/15
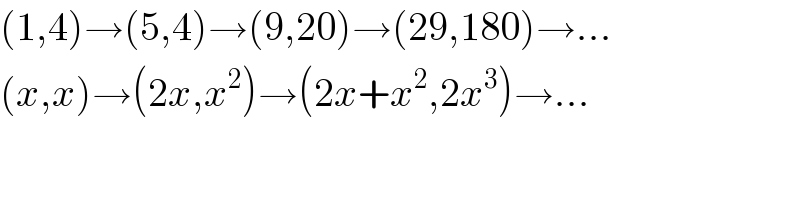
$$\left(\mathrm{1},\mathrm{4}\right)\rightarrow\left(\mathrm{5},\mathrm{4}\right)\rightarrow\left(\mathrm{9},\mathrm{20}\right)\rightarrow\left(\mathrm{29},\mathrm{180}\right)\rightarrow... \\ $$$$\left({x},{x}\right)\rightarrow\left(\mathrm{2}{x},{x}^{\mathrm{2}} \right)\rightarrow\left(\mathrm{2}{x}+{x}^{\mathrm{2}} ,\mathrm{2}{x}^{\mathrm{3}} \right)\rightarrow... \\ $$
Answered by Rasheed Soomro last updated on 13/Oct/15
![f(0,0)=0 [ ∵ f(x,y)=x,−2≤y≤2 and here x=0] Since f(x,y)=f(x+y,xy) Therefore f(1,4)=f(1+4,1.4)=f(5,4) =f(9,20)=f(29,180) , here ∣y∣≥100 f(29,180)=180 [∵ f(x,y)=y,∣x∣≥100∨∣y∣≥100 ] So, f(1,4)=f(29,180)=180 Continueing further in this way we can also find other values of f(1,4) f(1,4)=f(29,180)=f(209,5220)=5220 f(1,4)=180,5220,...](Q1845.png)
$$\:{f}\left(\mathrm{0},\mathrm{0}\right)=\mathrm{0}\:\:\:\:\left[\:\because\:\:{f}\left({x},{y}\right)={x},−\mathrm{2}\leqslant{y}\leqslant\mathrm{2}\:{and}\:{here}\:{x}=\mathrm{0}\right] \\ $$$${Since}\:{f}\left({x},{y}\right)={f}\left({x}+{y},{xy}\right) \\ $$$${Therefore}\:{f}\left(\mathrm{1},\mathrm{4}\right)={f}\left(\mathrm{1}+\mathrm{4},\mathrm{1}.\mathrm{4}\right)={f}\left(\mathrm{5},\mathrm{4}\right) \\ $$$$={f}\left(\mathrm{9},\mathrm{20}\right)={f}\left(\mathrm{29},\mathrm{180}\right)\:,\:{here}\:\mid{y}\mid\geqslant\mathrm{100}\: \\ $$$${f}\left(\mathrm{29},\mathrm{180}\right)=\mathrm{180}\:\:\left[\because\:\:\:{f}\left({x},{y}\right)={y},\mid{x}\mid\geqslant\mathrm{100}\vee\mid{y}\mid\geqslant\mathrm{100}\:\right] \\ $$$${So}, \\ $$$${f}\left(\mathrm{1},\mathrm{4}\right)={f}\left(\mathrm{29},\mathrm{180}\right)=\mathrm{180} \\ $$$${Continueing}\:{further}\:{in}\:{this}\:{way}\:{we}\:{can}\:{also}\:{find}\: \\ $$$${other}\:{values}\:{of}\:{f}\left(\mathrm{1},\mathrm{4}\right) \\ $$$${f}\left(\mathrm{1},\mathrm{4}\right)={f}\left(\mathrm{29},\mathrm{180}\right)={f}\left(\mathrm{209},\mathrm{5220}\right)=\mathrm{5220} \\ $$$${f}\left(\mathrm{1},\mathrm{4}\right)=\mathrm{180},\mathrm{5220},... \\ $$
