
Question Number 107674 by Study last updated on 12/Aug/20
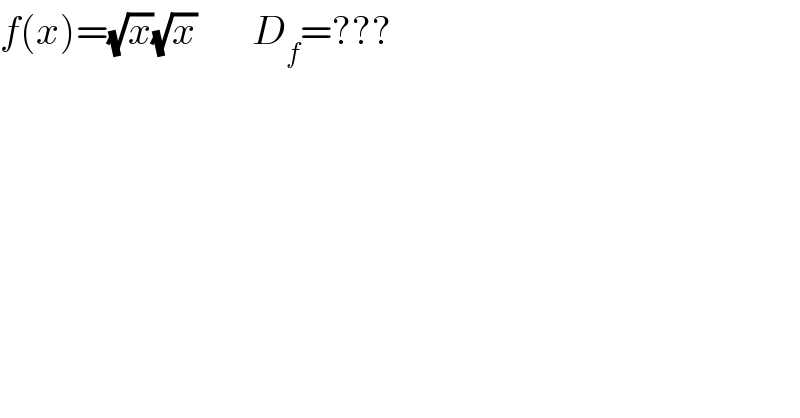
$${f}\left({x}\right)=\sqrt{{x}}\sqrt{{x}}\:\:\:\:\:\:\:{D}_{{f}} =??? \\ $$
Answered by Her_Majesty last updated on 12/Aug/20
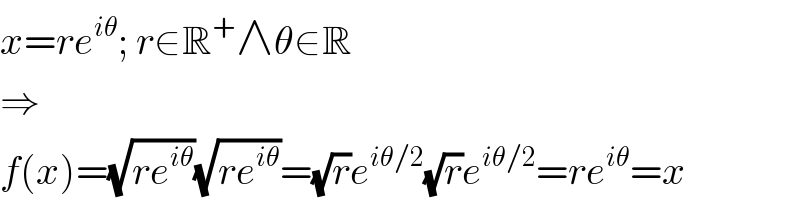
$${x}={re}^{{i}\theta} ;\:{r}\in\mathbb{R}^{+} \wedge\theta\in\mathbb{R} \\ $$$$\Rightarrow \\ $$$${f}\left({x}\right)=\sqrt{{re}^{{i}\theta} }\sqrt{{re}^{{i}\theta} }=\sqrt{{r}}{e}^{{i}\theta/\mathrm{2}} \sqrt{{r}}{e}^{{i}\theta/\mathrm{2}} ={re}^{{i}\theta} ={x} \\ $$
Answered by Her_Majesty last updated on 12/Aug/20
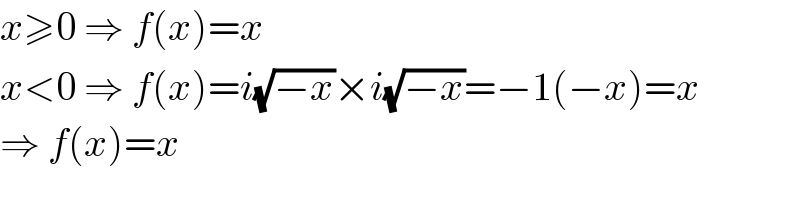
$${x}\geqslant\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)={x} \\ $$$${x}<\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)={i}\sqrt{−{x}}×{i}\sqrt{−{x}}=−\mathrm{1}\left(−{x}\right)={x} \\ $$$$\Rightarrow\:{f}\left({x}\right)={x} \\ $$
Commented by Study last updated on 12/Aug/20
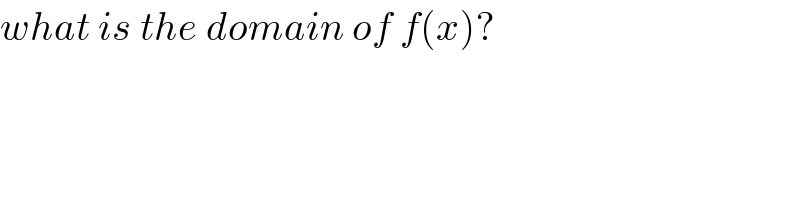
$${what}\:{is}\:{the}\:{domain}\:{of}\:{f}\left({x}\right)? \\ $$
Commented by Her_Majesty last updated on 12/Aug/20

$${if}\:{we}\:{stay}\:{in}\:\mathbb{R}\:{the}\:{domain}\:{is}\:{x}\geqslant\mathrm{0} \\ $$
