Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 48208 by naka3546 last updated on 20/Nov/18

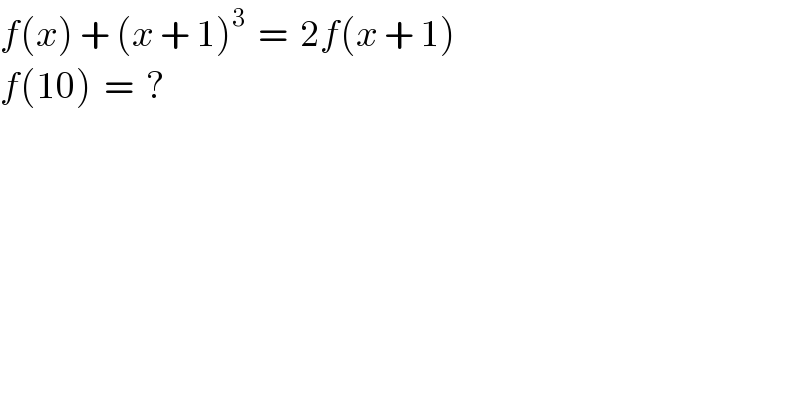
f(x) + (x + 1)^3 = 2f(x + 1) f(10) = ?

$${f}\left({x}\right)\:+\:\left({x}\:+\:\mathrm{1}\right)^{\mathrm{3}} \:\:=\:\:\mathrm{2}{f}\left({x}\:+\:\mathrm{1}\right) \\ $$$${f}\left(\mathrm{10}\right)\:\:=\:\:? \\ $$

Answered by MJS last updated on 20/Nov/18

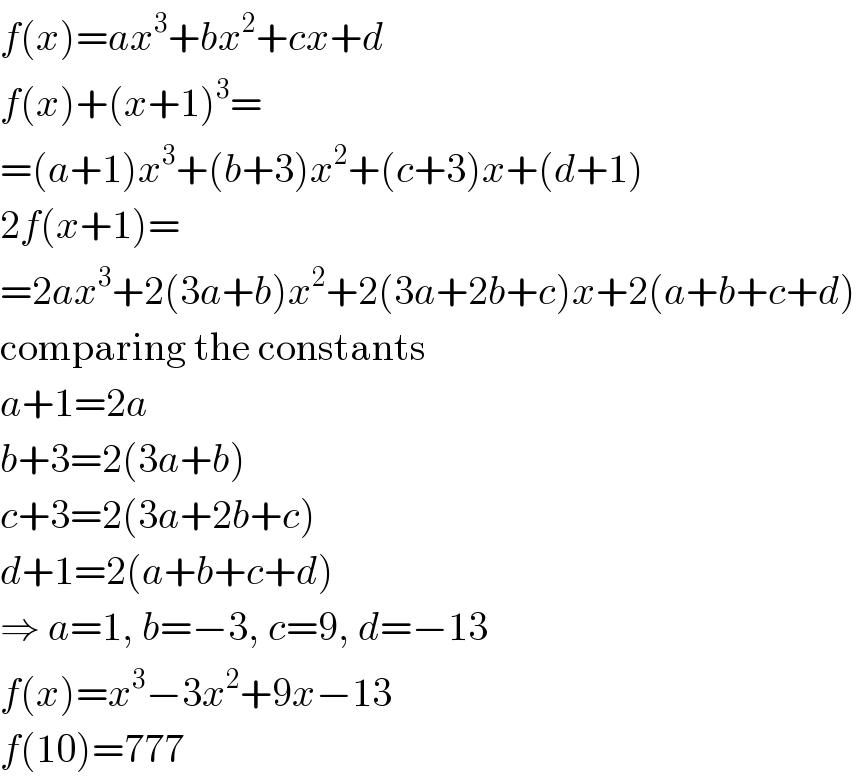
f(x)=ax^3 +bx^2 +cx+d f(x)+(x+1)^3 = =(a+1)x^3 +(b+3)x^2 +(c+3)x+(d+1) 2f(x+1)= =2ax^3 +2(3a+b)x^2 +2(3a+2b+c)x+2(a+b+c+d) comparing the constants a+1=2a b+3=2(3a+b) c+3=2(3a+2b+c) d+1=2(a+b+c+d) ⇒ a=1, b=−3, c=9, d=−13 f(x)=x^3 −3x^2 +9x−13 f(10)=777

$${f}\left({x}\right)={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${f}\left({x}\right)+\left({x}+\mathrm{1}\right)^{\mathrm{3}} = \\ $$$$=\left({a}+\mathrm{1}\right){x}^{\mathrm{3}} +\left({b}+\mathrm{3}\right){x}^{\mathrm{2}} +\left({c}+\mathrm{3}\right){x}+\left({d}+\mathrm{1}\right) \\ $$$$\mathrm{2}{f}\left({x}+\mathrm{1}\right)= \\ $$$$=\mathrm{2}{ax}^{\mathrm{3}} +\mathrm{2}\left(\mathrm{3}{a}+{b}\right){x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}{a}+\mathrm{2}{b}+{c}\right){x}+\mathrm{2}\left({a}+{b}+{c}+{d}\right) \\ $$$$\mathrm{comparing}\:\mathrm{the}\:\mathrm{constants} \\ $$$${a}+\mathrm{1}=\mathrm{2}{a} \\ $$$${b}+\mathrm{3}=\mathrm{2}\left(\mathrm{3}{a}+{b}\right) \\ $$$${c}+\mathrm{3}=\mathrm{2}\left(\mathrm{3}{a}+\mathrm{2}{b}+{c}\right) \\ $$$${d}+\mathrm{1}=\mathrm{2}\left({a}+{b}+{c}+{d}\right) \\ $$$$\Rightarrow\:{a}=\mathrm{1},\:{b}=−\mathrm{3},\:{c}=\mathrm{9},\:{d}=−\mathrm{13} \\ $$$${f}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}−\mathrm{13} \\ $$$${f}\left(\mathrm{10}\right)=\mathrm{777} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com