Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 206882 by efronzo1 last updated on 29/Apr/24

f(x)=tan^2 x (√(tan x((tan x((tan x((tan x(√(...))))^(1/5) ))^(1/4) ))^(1/3) )) f ′((π/4))=?

$$\:\:{f}\left({x}\right)=\mathrm{tan}\:^{\mathrm{2}} {x}\:\sqrt{\mathrm{tan}\:{x}\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}\sqrt[{\mathrm{4}}]{\mathrm{tan}\:{x}\sqrt[{\mathrm{5}}]{\mathrm{tan}\:{x}\sqrt{...}}}}} \\ $$$$\:{f}\:'\left(\frac{\pi}{\mathrm{4}}\right)=? \\ $$

Answered by MM42 last updated on 29/Apr/24

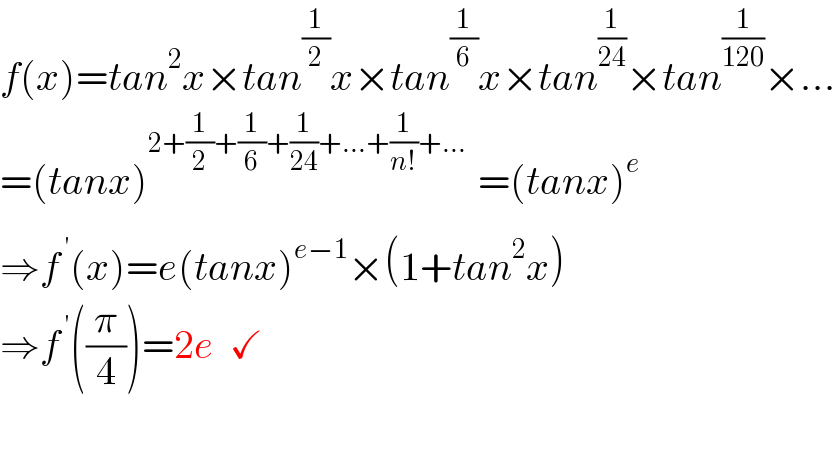
f(x)=tan^2 x×tan^(1/2) x×tan^(1/6) x×tan^(1/(24)) ×tan^(1/(120)) ×... =(tanx)_ ^(2+(1/2)+(1/6)+(1/(24))+...+(1/(n!))+... ) =(tanx)^e ⇒f^( ′) (x)=e(tanx)^(e−1) ×(1+tan^2 x) ⇒f^( ′) ((π/4))=2e ✓

$${f}\left({x}\right)={tan}^{\mathrm{2}} {x}×{tan}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}×{tan}^{\frac{\mathrm{1}}{\mathrm{6}}} {x}×{tan}^{\frac{\mathrm{1}}{\mathrm{24}}} ×{tan}^{\frac{\mathrm{1}}{\mathrm{120}}} ×... \\ $$$$=\left({tanx}\right)_{} ^{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{24}}+...+\frac{\mathrm{1}}{{n}!}+...\:\:\:} =\left({tanx}\right)^{{e}} \\ $$$$\Rightarrow{f}^{\:'} \left({x}\right)={e}\left({tanx}\right)^{{e}−\mathrm{1}} ×\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right) \\ $$$$\Rightarrow{f}^{\:'} \left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{2}{e}\:\:\checkmark \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com