Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 830 by prakash jain last updated on 20/Mar/15

f(x) is a polynomial such that f(x^2 )=f(x)f(x−1) Find f(x) such that f(x)≠0.

$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{such}\:\mathrm{that} \\ $$$${f}\left({x}^{\mathrm{2}} \right)={f}\left({x}\right){f}\left({x}−\mathrm{1}\right) \\ $$$$\mathrm{Find}\:{f}\left({x}\right)\:\mathrm{such}\:\mathrm{that}\:{f}\left({x}\right)\neq\mathrm{0}. \\ $$

Commented by 123456 last updated on 23/Mar/15

f(x)=Σ_(i=0) ^n a_i x^i f(x^2 )=Σ_(i=0) ^n a_i x^(2i) ≡Σ_(i=0) ^(2n) b_i x^i f(x−1)=Σ_(i=0) ^n a_i (x−1)^i =Σ_(i=0) ^n c_i x^i f(x)f(x−1)=Σ_(i=0) ^n a_i x^i Σ_(i=0) ^n c_i x^i =Σ_(i=0) ^(2n) d_i x^i b_i = { (a_(i/2) ,(i≡0(mod 2))),(0,(i≡1(mod 2))) :} (x−1)^i =Σ_(j=0) ^i ((i),(j) ) x^j (−1)^(i−j) Σ_(i=0) ^n a_i (x−1)^i =Σ_(i=0) ^n a_i Σ_(j=0) ^i ((i),(j) ) x^j (−1)^(i−j) =Σ_(i=0) ^n c_i x^i c_i =^? Σ_(j=i) ^n ((j),(i) )(−1)^(j−i) a_j d_i =Σ_(j=0) ^i a_j c_(i−j) d_i =b_i

$${f}\left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{{i}} \\ $$$${f}\left({x}^{\mathrm{2}} \right)=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{\mathrm{2}{i}} \equiv\underset{{i}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{b}_{{i}} {x}^{{i}} \\ $$$${f}\left({x}−\mathrm{1}\right)=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} \left({x}−\mathrm{1}\right)^{{i}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{c}_{{i}} {x}^{{i}} \\ $$$${f}\left({x}\right){f}\left({x}−\mathrm{1}\right)=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{{i}} \underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{c}_{{i}} {x}^{{i}} =\underset{{i}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{d}_{{i}} {x}^{{i}} \\ $$$${b}_{{i}} =\begin{cases}{{a}_{{i}/\mathrm{2}} }&{{i}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right)}\\{\mathrm{0}}&{{i}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right)}\end{cases} \\ $$$$\left({x}−\mathrm{1}\right)^{{i}} =\underset{{j}=\mathrm{0}} {\overset{{i}} {\sum}}\begin{pmatrix}{{i}}\\{{j}}\end{pmatrix}\:{x}^{{j}} \left(−\mathrm{1}\right)^{{i}−{j}} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} \left({x}−\mathrm{1}\right)^{{i}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} \underset{{j}=\mathrm{0}} {\overset{{i}} {\sum}}\begin{pmatrix}{{i}}\\{{j}}\end{pmatrix}\:{x}^{{j}} \left(−\mathrm{1}\right)^{{i}−{j}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{c}_{{i}} {x}^{{i}} \\ $$$${c}_{{i}} \overset{?} {=}\underset{{j}={i}} {\overset{{n}} {\sum}}\begin{pmatrix}{{j}}\\{{i}}\end{pmatrix}\left(−\mathrm{1}\right)^{{j}−{i}} {a}_{{j}} \\ $$$${d}_{{i}} =\underset{{j}=\mathrm{0}} {\overset{{i}} {\sum}}{a}_{{j}} {c}_{{i}−{j}} \\ $$$${d}_{{i}} ={b}_{{i}} \\ $$

Commented by 123456 last updated on 23/Mar/15

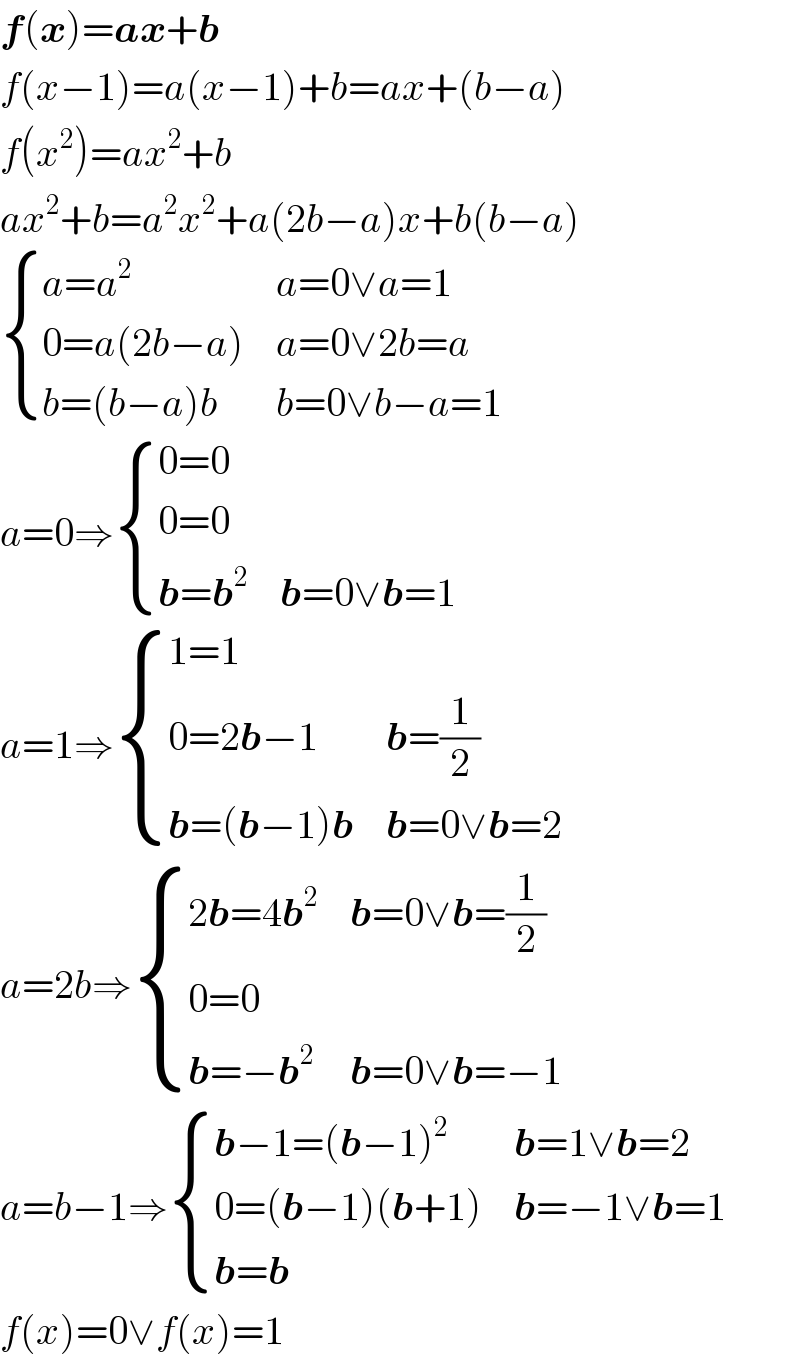
f(x)=ax+b f(x−1)=a(x−1)+b=ax+(b−a) f(x^2 )=ax^2 +b ax^2 +b=a^2 x^2 +a(2b−a)x+b(b−a) { ((a=a^2 ),(a=0∨a=1)),((0=a(2b−a)),(a=0∨2b=a)),((b=(b−a)b),(b=0∨b−a=1)) :} a=0⇒ { ((0=0),),((0=0),),((b=b^2 ),(b=0∨b=1)) :} a=1⇒ { ((1=1),),((0=2b−1),(b=(1/2))),((b=(b−1)b),(b=0∨b=2)) :} a=2b⇒ { ((2b=4b^2 ),(b=0∨b=(1/2))),((0=0),),((b=−b^2 ),(b=0∨b=−1)) :} a=b−1⇒ { ((b−1=(b−1)^2 ),(b=1∨b=2)),((0=(b−1)(b+1)),(b=−1∨b=1)),((b=b),) :} f(x)=0∨f(x)=1

$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{ax}}+\boldsymbol{{b}} \\ $$$${f}\left({x}−\mathrm{1}\right)={a}\left({x}−\mathrm{1}\right)+{b}={ax}+\left({b}−{a}\right) \\ $$$${f}\left({x}^{\mathrm{2}} \right)={ax}^{\mathrm{2}} +{b} \\ $$$${ax}^{\mathrm{2}} +{b}={a}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}\left(\mathrm{2}{b}−{a}\right){x}+{b}\left({b}−{a}\right) \\ $$$$\begin{cases}{{a}={a}^{\mathrm{2}} }&{{a}=\mathrm{0}\vee{a}=\mathrm{1}}\\{\mathrm{0}={a}\left(\mathrm{2}{b}−{a}\right)}&{{a}=\mathrm{0}\vee\mathrm{2}{b}={a}}\\{{b}=\left({b}−{a}\right){b}}&{{b}=\mathrm{0}\vee{b}−{a}=\mathrm{1}}\end{cases} \\ $$$${a}=\mathrm{0}\Rightarrow\begin{cases}{\mathrm{0}=\mathrm{0}}&{}\\{\mathrm{0}=\mathrm{0}}&{}\\{\boldsymbol{{b}}=\boldsymbol{{b}}^{\mathrm{2}} }&{\boldsymbol{{b}}=\mathrm{0}\vee\boldsymbol{{b}}=\mathrm{1}}\end{cases} \\ $$$${a}=\mathrm{1}\Rightarrow\begin{cases}{\mathrm{1}=\mathrm{1}}&{}\\{\mathrm{0}=\mathrm{2}\boldsymbol{{b}}−\mathrm{1}}&{\boldsymbol{{b}}=\frac{\mathrm{1}}{\mathrm{2}}}\\{\boldsymbol{{b}}=\left(\boldsymbol{{b}}−\mathrm{1}\right)\boldsymbol{{b}}}&{\boldsymbol{{b}}=\mathrm{0}\vee\boldsymbol{{b}}=\mathrm{2}}\end{cases} \\ $$$${a}=\mathrm{2}{b}\Rightarrow\begin{cases}{\mathrm{2}\boldsymbol{{b}}=\mathrm{4}\boldsymbol{{b}}^{\mathrm{2}} }&{\boldsymbol{{b}}=\mathrm{0}\vee\boldsymbol{{b}}=\frac{\mathrm{1}}{\mathrm{2}}}\\{\mathrm{0}=\mathrm{0}}&{}\\{\boldsymbol{{b}}=−\boldsymbol{{b}}^{\mathrm{2}} }&{\boldsymbol{{b}}=\mathrm{0}\vee\boldsymbol{{b}}=−\mathrm{1}}\end{cases} \\ $$$${a}={b}−\mathrm{1}\Rightarrow\begin{cases}{\boldsymbol{{b}}−\mathrm{1}=\left(\boldsymbol{{b}}−\mathrm{1}\right)^{\mathrm{2}} }&{\boldsymbol{{b}}=\mathrm{1}\vee\boldsymbol{{b}}=\mathrm{2}}\\{\mathrm{0}=\left(\boldsymbol{{b}}−\mathrm{1}\right)\left(\boldsymbol{{b}}+\mathrm{1}\right)}&{\boldsymbol{{b}}=−\mathrm{1}\vee\boldsymbol{{b}}=\mathrm{1}}\\{\boldsymbol{{b}}=\boldsymbol{{b}}}&{}\end{cases} \\ $$$${f}\left({x}\right)=\mathrm{0}\vee{f}\left({x}\right)=\mathrm{1} \\ $$

Commented by 123456 last updated on 23/Mar/15

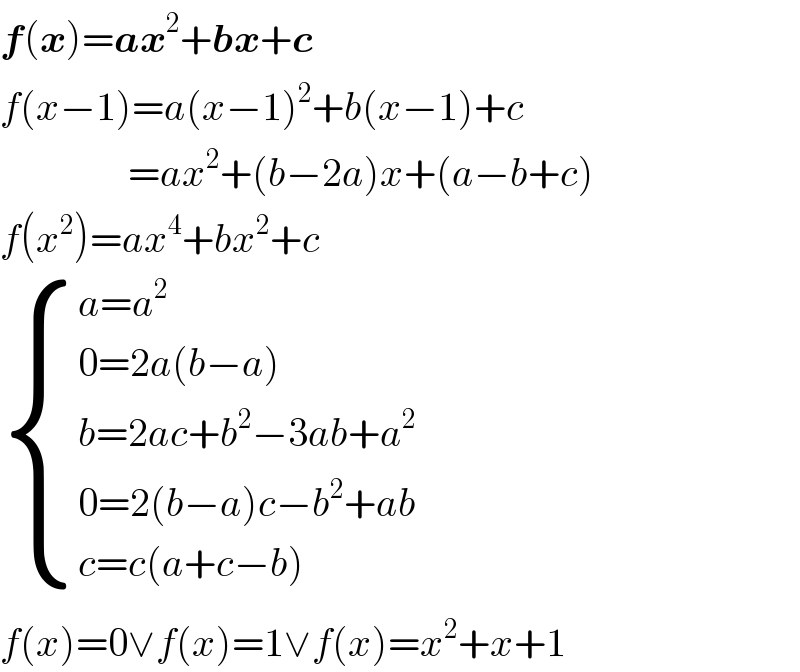
f(x)=ax^2 +bx+c f(x−1)=a(x−1)^2 +b(x−1)+c =ax^2 +(b−2a)x+(a−b+c) f(x^2 )=ax^4 +bx^2 +c { ((a=a^2 )),((0=2a(b−a))),((b=2ac+b^2 −3ab+a^2 )),((0=2(b−a)c−b^2 +ab)),((c=c(a+c−b))) :} f(x)=0∨f(x)=1∨f(x)=x^2 +x+1

$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{ax}}^{\mathrm{2}} +\boldsymbol{{bx}}+\boldsymbol{{c}} \\ $$$${f}\left({x}−\mathrm{1}\right)={a}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{b}\left({x}−\mathrm{1}\right)+{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ax}^{\mathrm{2}} +\left({b}−\mathrm{2}{a}\right){x}+\left({a}−{b}+{c}\right) \\ $$$${f}\left({x}^{\mathrm{2}} \right)={ax}^{\mathrm{4}} +{bx}^{\mathrm{2}} +{c} \\ $$$$\begin{cases}{{a}={a}^{\mathrm{2}} }\\{\mathrm{0}=\mathrm{2}{a}\left({b}−{a}\right)}\\{{b}=\mathrm{2}{ac}+{b}^{\mathrm{2}} −\mathrm{3}{ab}+{a}^{\mathrm{2}} }\\{\mathrm{0}=\mathrm{2}\left({b}−{a}\right){c}−{b}^{\mathrm{2}} +{ab}}\\{{c}={c}\left({a}+{c}−{b}\right)}\end{cases} \\ $$$${f}\left({x}\right)=\mathrm{0}\vee{f}\left({x}\right)=\mathrm{1}\vee{f}\left({x}\right)={x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$

Commented by 123456 last updated on 23/Mar/15

suppose that f_1 (x) is a solution and f(x)=f_1 (x)+f_2 (x) is also a solution f(x^2 )=f(x)f(x−1) f_1 (x^2 )+f_2 (x^2 )=[f_1 (x)+f_2 (x)][f_1 (x−1)+f_2 (x−1)] =f_1 (x)f_1 (x−1)+f_1 (x)f_2 (x−1)+f_2 (x)f_1 (x−1)+f_2 (x)f_2 (x−1) f_2 (x^2 )=f_1 (x)f_2 (x−1)+f_2 (x)f_1 (x−1)+f_2 (x)f_2 (x−1) f_1 (x)=0⇒f_2 (x^2 )=f_2 (x)f_2 (x−1) f_1 (x)=1⇒f_2 (x^2 )=f_2 (x−1)+f_2 (x)+f_2 (x−1)f_2 (x−1)

$$\mathrm{suppose}\:\mathrm{that}\:{f}_{\mathrm{1}} \left({x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{and} \\ $$$${f}\left({x}\right)={f}_{\mathrm{1}} \left({x}\right)+{f}_{\mathrm{2}} \left({x}\right)\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{solution} \\ $$$${f}\left({x}^{\mathrm{2}} \right)={f}\left({x}\right){f}\left({x}−\mathrm{1}\right) \\ $$$${f}_{\mathrm{1}} \left({x}^{\mathrm{2}} \right)+{f}_{\mathrm{2}} \left({x}^{\mathrm{2}} \right)=\left[{f}_{\mathrm{1}} \left({x}\right)+{f}_{\mathrm{2}} \left({x}\right)\right]\left[{f}_{\mathrm{1}} \left({x}−\mathrm{1}\right)+{f}_{\mathrm{2}} \left({x}−\mathrm{1}\right)\right] \\ $$$$={f}_{\mathrm{1}} \left({x}\right){f}_{\mathrm{1}} \left({x}−\mathrm{1}\right)+{f}_{\mathrm{1}} \left({x}\right){f}_{\mathrm{2}} \left({x}−\mathrm{1}\right)+{f}_{\mathrm{2}} \left({x}\right){f}_{\mathrm{1}} \left({x}−\mathrm{1}\right)+{f}_{\mathrm{2}} \left({x}\right){f}_{\mathrm{2}} \left({x}−\mathrm{1}\right) \\ $$$${f}_{\mathrm{2}} \left({x}^{\mathrm{2}} \right)={f}_{\mathrm{1}} \left({x}\right){f}_{\mathrm{2}} \left({x}−\mathrm{1}\right)+{f}_{\mathrm{2}} \left({x}\right){f}_{\mathrm{1}} \left({x}−\mathrm{1}\right)+{f}_{\mathrm{2}} \left({x}\right){f}_{\mathrm{2}} \left({x}−\mathrm{1}\right) \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\mathrm{0}\Rightarrow{f}_{\mathrm{2}} \left({x}^{\mathrm{2}} \right)={f}_{\mathrm{2}} \left({x}\right){f}_{\mathrm{2}} \left({x}−\mathrm{1}\right) \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\mathrm{1}\Rightarrow{f}_{\mathrm{2}} \left({x}^{\mathrm{2}} \right)={f}_{\mathrm{2}} \left({x}−\mathrm{1}\right)+{f}_{\mathrm{2}} \left({x}\right)+{f}_{\mathrm{2}} \left({x}−\mathrm{1}\right){f}_{\mathrm{2}} \left({x}−\mathrm{1}\right) \\ $$

Commented by prakash jain last updated on 23/Mar/15

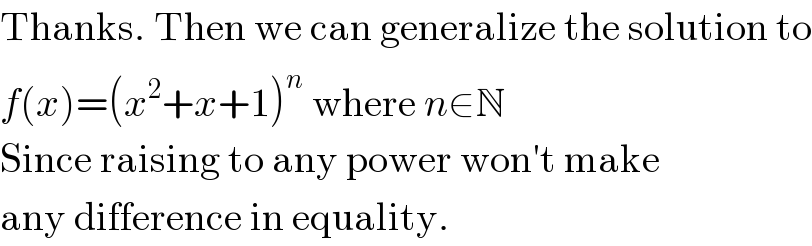
Thanks. Then we can generalize the solution to f(x)=(x^2 +x+1)^n where n∈N Since raising to any power won′t make any difference in equality.

$$\mathrm{Thanks}.\:\mathrm{Then}\:\mathrm{we}\:\mathrm{can}\:\mathrm{generalize}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{to} \\ $$$${f}\left({x}\right)=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{{n}} \:\mathrm{where}\:{n}\in\mathbb{N} \\ $$$$\mathrm{Since}\:\mathrm{raising}\:\mathrm{to}\:\mathrm{any}\:\mathrm{power}\:\mathrm{won}'\mathrm{t}\:\mathrm{make} \\ $$$$\mathrm{any}\:\mathrm{difference}\:\mathrm{in}\:\mathrm{equality}. \\ $$

Commented by prakash jain last updated on 23/Mar/15

x^4 +x^2 +1=(x^2 +x+1)(x^2 −2x+1+x−1+1) =(x^2 +x+1)(x^2 −x+1)

$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}+{x}−\mathrm{1}+\mathrm{1}\right) \\ $$$$=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com