Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 216820 by Ismoiljon_008 last updated on 22/Feb/25

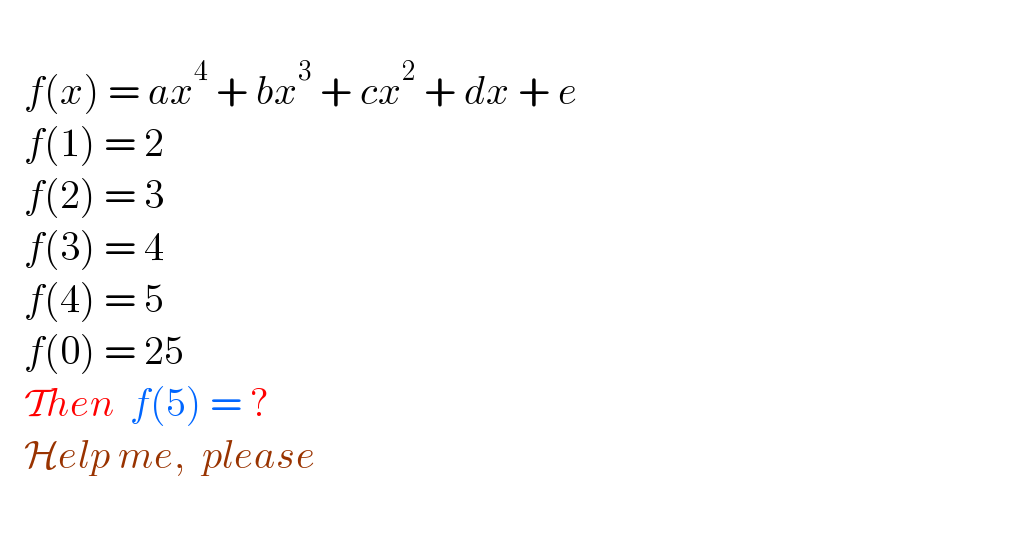
f(x) = ax^4 + bx^3 + cx^2 + dx + e f(1) = 2 f(2) = 3 f(3) = 4 f(4) = 5 f(0) = 25 Then f(5) = ? Help me, please

$$ \\ $$$$\:\:\:{f}\left({x}\right)\:=\:{ax}^{\mathrm{4}} \:+\:{bx}^{\mathrm{3}} \:+\:{cx}^{\mathrm{2}} \:+\:{dx}\:+\:{e} \\ $$$$\:\:\:{f}\left(\mathrm{1}\right)\:=\:\mathrm{2} \\ $$$$\:\:\:{f}\left(\mathrm{2}\right)\:=\:\mathrm{3} \\ $$$$\:\:\:{f}\left(\mathrm{3}\right)\:=\:\mathrm{4} \\ $$$$\:\:\:{f}\left(\mathrm{4}\right)\:=\:\mathrm{5}\: \\ $$$$\:\:\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{25} \\ $$$$\:\:\:\mathcal{T}{hen}\:\:{f}\left(\mathrm{5}\right)\:=\:? \\ $$$$\:\:\:\mathcal{H}{elp}\:{me},\:\:{please} \\ $$$$ \\ $$

Answered by BaliramKumar last updated on 22/Feb/25

Commented by Ismoiljon_008 last updated on 22/Feb/25

thank you very much

$$\:\:\:{thank}\:{you}\:{very}\:{much} \\ $$

Commented by ArshadS last updated on 22/Feb/25

Some explanation please!

$$\mathrm{Some}\:\mathrm{explanation}\:\mathrm{please}! \\ $$

Answered by mr W last updated on 22/Feb/25

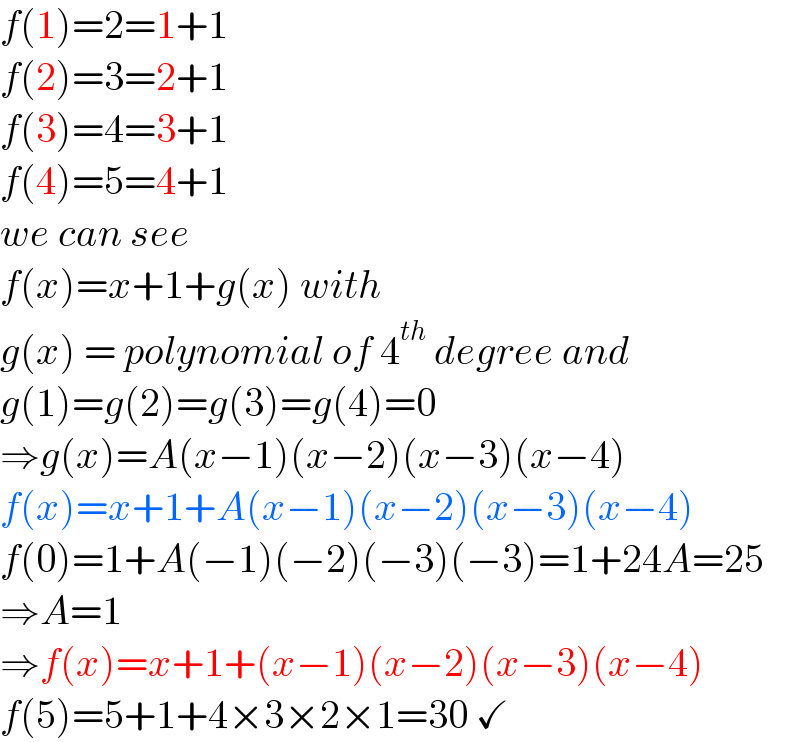
f(1)=2=1+1 f(2)=3=2+1 f(3)=4=3+1 f(4)=5=4+1 we can see f(x)=x+1+g(x) with g(x) = polynomial of 4^(th) degree and g(1)=g(2)=g(3)=g(4)=0 ⇒g(x)=A(x−1)(x−2)(x−3)(x−4) f(x)=x+1+A(x−1)(x−2)(x−3)(x−4) f(0)=1+A(−1)(−2)(−3)(−3)=1+24A=25 ⇒A=1 ⇒f(x)=x+1+(x−1)(x−2)(x−3)(x−4) f(5)=5+1+4×3×2×1=30 ✓

$${f}\left(\mathrm{1}\right)=\mathrm{2}=\mathrm{1}+\mathrm{1} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{3}=\mathrm{2}+\mathrm{1} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{4}=\mathrm{3}+\mathrm{1} \\ $$$${f}\left(\mathrm{4}\right)=\mathrm{5}=\mathrm{4}+\mathrm{1} \\ $$$${we}\:{can}\:{see} \\ $$$${f}\left({x}\right)={x}+\mathrm{1}+{g}\left({x}\right)\:{with}\: \\ $$$${g}\left({x}\right)\:=\:{polynomial}\:{of}\:\mathrm{4}^{{th}} \:{degree}\:{and} \\ $$$${g}\left(\mathrm{1}\right)={g}\left(\mathrm{2}\right)={g}\left(\mathrm{3}\right)={g}\left(\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow{g}\left({x}\right)={A}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right) \\ $$$${f}\left({x}\right)={x}+\mathrm{1}+{A}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1}+{A}\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)\left(−\mathrm{3}\right)=\mathrm{1}+\mathrm{24}{A}=\mathrm{25}\: \\ $$$$\Rightarrow{A}=\mathrm{1} \\ $$$$\Rightarrow{f}\left({x}\right)={x}+\mathrm{1}+\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right) \\ $$$${f}\left(\mathrm{5}\right)=\mathrm{5}+\mathrm{1}+\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}=\mathrm{30}\:\checkmark \\ $$

Commented by ArshadS last updated on 23/Feb/25

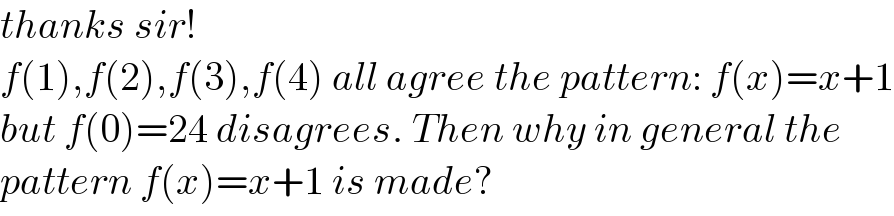
thanks sir! f(1),f(2),f(3),f(4) all agree the pattern: f(x)=x+1 but f(0)=24 disagrees. Then why in general the pattern f(x)=x+1 is made?

$${thanks}\:{sir}! \\ $$$${f}\left(\mathrm{1}\right),{f}\left(\mathrm{2}\right),{f}\left(\mathrm{3}\right),{f}\left(\mathrm{4}\right)\:{all}\:{agree}\:{the}\:{pattern}:\:{f}\left({x}\right)={x}+\mathrm{1} \\ $$$${but}\:{f}\left(\mathrm{0}\right)=\mathrm{24}\:{disagrees}.\:{Then}\:{why}\:{in}\:{general}\:{the} \\ $$$${pattern}\:{f}\left({x}\right)={x}+\mathrm{1}\:{is}\:{made}? \\ $$

Commented by mr W last updated on 23/Feb/25

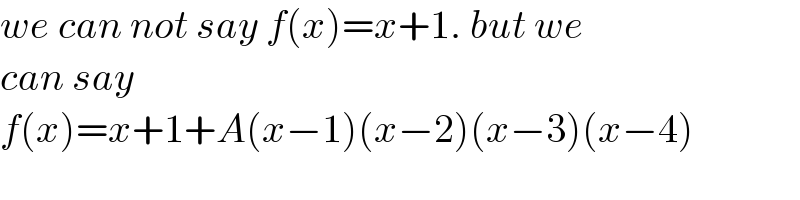
we can not say f(x)=x+1. but we can say f(x)=x+1+A(x−1)(x−2)(x−3)(x−4)

$${we}\:{can}\:{not}\:{say}\:{f}\left({x}\right)={x}+\mathrm{1}.\:{but}\:{we} \\ $$$${can}\:{say} \\ $$$${f}\left({x}\right)={x}+\mathrm{1}+{A}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right) \\ $$

Commented by ArshadS last updated on 23/Feb/25

Thanks to teach me sir!

$$\mathcal{T}{hanks}\:{to}\:{teach}\:{me}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com