
Question Number 165949 by mathlove last updated on 10/Feb/22
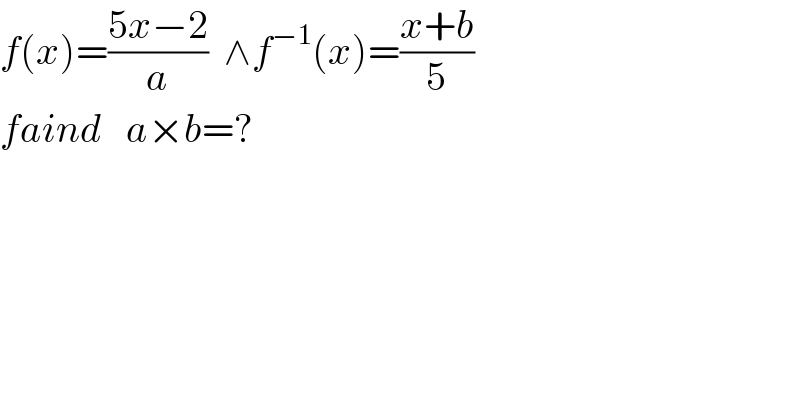
$${f}\left({x}\right)=\frac{\mathrm{5}{x}−\mathrm{2}}{{a}}\:\:\wedge{f}^{−\mathrm{1}} \left({x}\right)=\frac{{x}+{b}}{\mathrm{5}} \\ $$$${faind}\:\:\:{a}×{b}=? \\ $$
Answered by qaz last updated on 10/Feb/22

$$\left(\frac{\mathrm{5x}−\mathrm{2}}{\mathrm{a}}\right)'\centerdot\left(\frac{\mathrm{x}+\mathrm{b}}{\mathrm{5}}\right)'=\frac{\mathrm{1}}{\mathrm{a}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{a}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{5x}−\mathrm{2} \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\mathrm{2}+\mathrm{x}}{\mathrm{5}}=\frac{\mathrm{x}+\mathrm{b}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{b}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{a}×\mathrm{b}=\mathrm{2} \\ $$
Answered by cortano1 last updated on 10/Feb/22
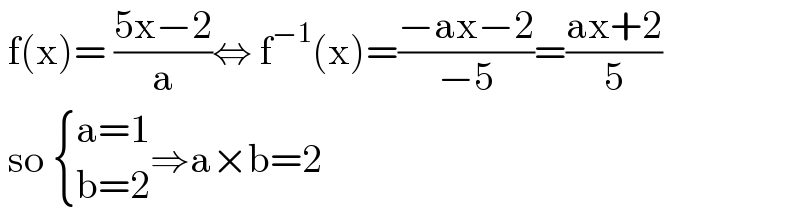
$$\:\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{5x}−\mathrm{2}}{\mathrm{a}}\Leftrightarrow\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{−\mathrm{ax}−\mathrm{2}}{−\mathrm{5}}=\frac{\mathrm{ax}+\mathrm{2}}{\mathrm{5}} \\ $$$$\:\mathrm{so}\:\begin{cases}{\mathrm{a}=\mathrm{1}}\\{\mathrm{b}=\mathrm{2}}\end{cases}\Rightarrow\mathrm{a}×\mathrm{b}=\mathrm{2} \\ $$
