
Question Number 147980 by mathdanisur last updated on 24/Jul/21
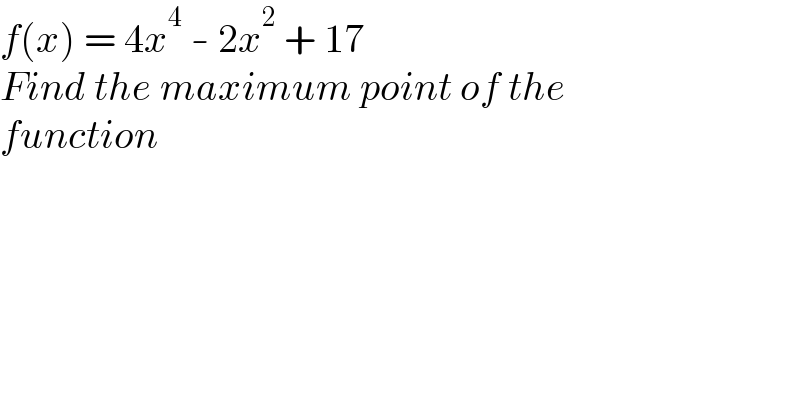
$${f}\left({x}\right)\:=\:\mathrm{4}{x}^{\mathrm{4}} \:-\:\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{17} \\ $$$${Find}\:{the}\:{maximum}\:{point}\:{of}\:{the} \\ $$$${function} \\ $$
Answered by iloveisrael last updated on 25/Jul/21
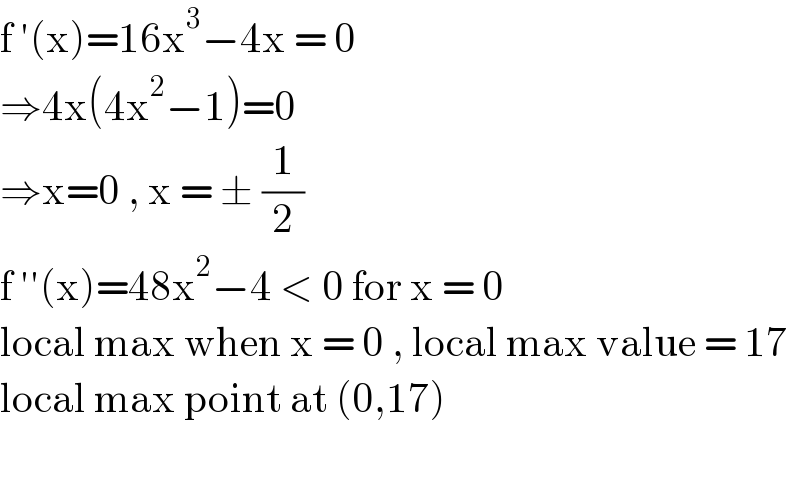
$$\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{16x}^{\mathrm{3}} −\mathrm{4x}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{4x}\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{0}\:,\:\mathrm{x}\:=\:\pm\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{f}\:''\left(\mathrm{x}\right)=\mathrm{48x}^{\mathrm{2}} −\mathrm{4}\:<\:\mathrm{0}\:\mathrm{for}\:\mathrm{x}\:=\:\mathrm{0} \\ $$$$\mathrm{local}\:\mathrm{max}\:\mathrm{when}\:\mathrm{x}\:=\:\mathrm{0}\:,\:\mathrm{local}\:\mathrm{max}\:\mathrm{value}\:=\:\mathrm{17} \\ $$$$\mathrm{local}\:\mathrm{max}\:\mathrm{point}\:\mathrm{at}\:\left(\mathrm{0},\mathrm{17}\right)\: \\ $$$$ \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thanks}\:{Ser} \\ $$
