Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 130354 by greg_ed last updated on 24/Jan/21

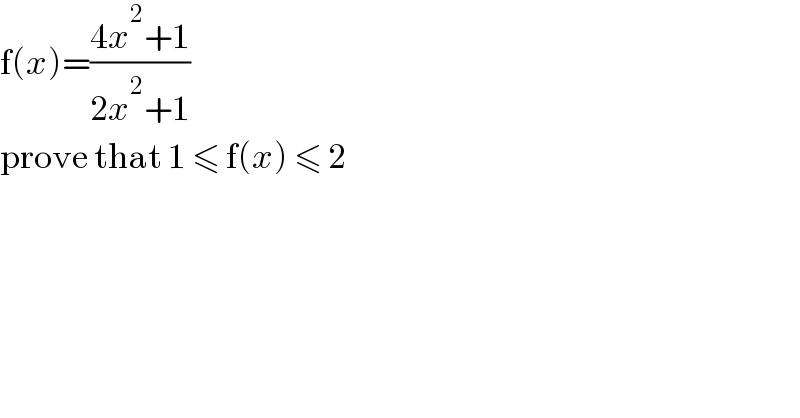
f(x)=((4x^2 +1)/(2x^2 +1)) prove that 1 ≤ f(x) ≤ 2

$$\mathrm{f}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{1}\:\leqslant\:\mathrm{f}\left({x}\right)\:\leqslant\:\mathrm{2} \\ $$

Answered by MJS_new last updated on 24/Jan/21

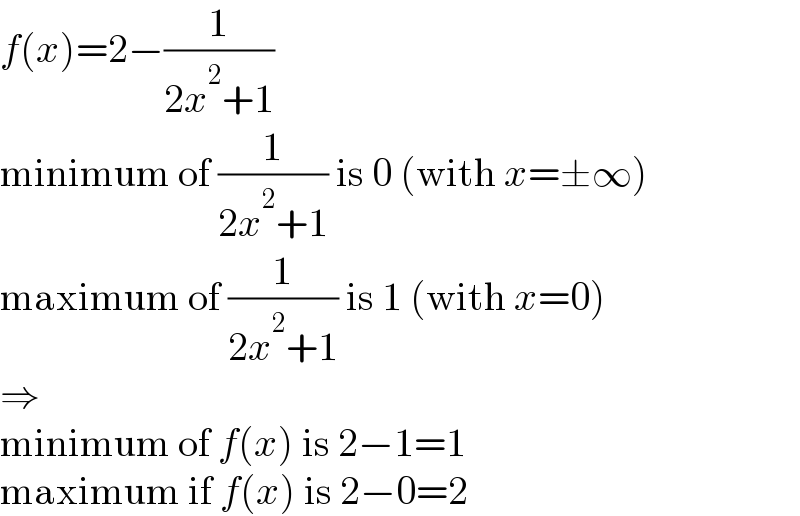
f(x)=2−(1/(2x^2 +1)) minimum of (1/(2x^2 +1)) is 0 (with x=±∞) maximum of (1/(2x^2 +1)) is 1 (with x=0) ⇒ minimum of f(x) is 2−1=1 maximum if f(x) is 2−0=2

$${f}\left({x}\right)=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{minimum}\:\mathrm{of}\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{is}\:\mathrm{0}\:\left(\mathrm{with}\:{x}=\pm\infty\right) \\ $$$$\mathrm{maximum}\:\mathrm{of}\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{is}\:\mathrm{1}\:\left(\mathrm{with}\:{x}=\mathrm{0}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{minimum}\:\mathrm{of}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{2}−\mathrm{1}=\mathrm{1} \\ $$$$\mathrm{maximum}\:\mathrm{if}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{2}−\mathrm{0}=\mathrm{2} \\ $$

Answered by ajfour last updated on 24/Jan/21

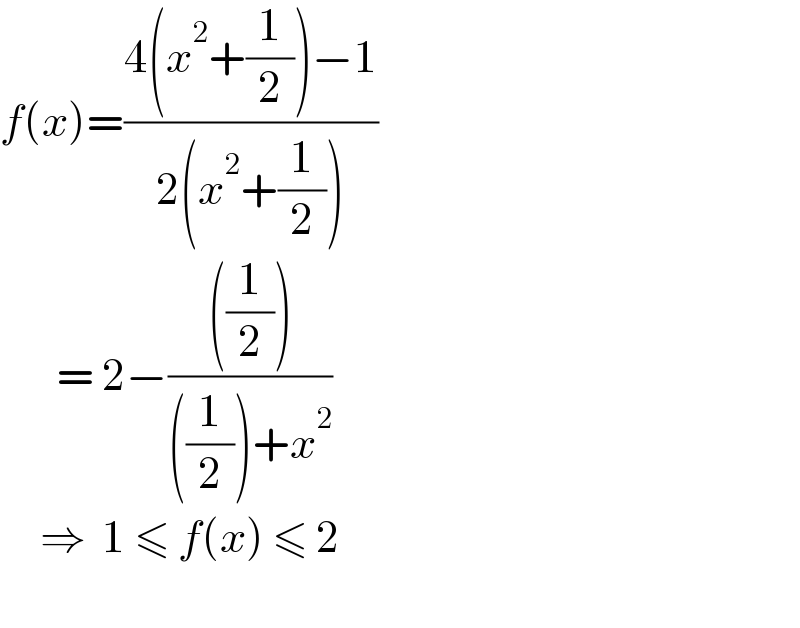
f(x)=((4(x^2 +(1/2))−1)/(2(x^2 +(1/2)))) = 2−((((1/2)))/(((1/2))+x^2 )) ⇒ 1 ≤ f(x) ≤ 2

$${f}\left({x}\right)=\frac{\mathrm{4}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{2}−\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\Rightarrow\:\:\mathrm{1}\:\leqslant\:{f}\left({x}\right)\:\leqslant\:\mathrm{2} \\ $$$$ \\ $$

Answered by nueron last updated on 24/Jan/21

Answered by Olaf last updated on 24/Jan/21

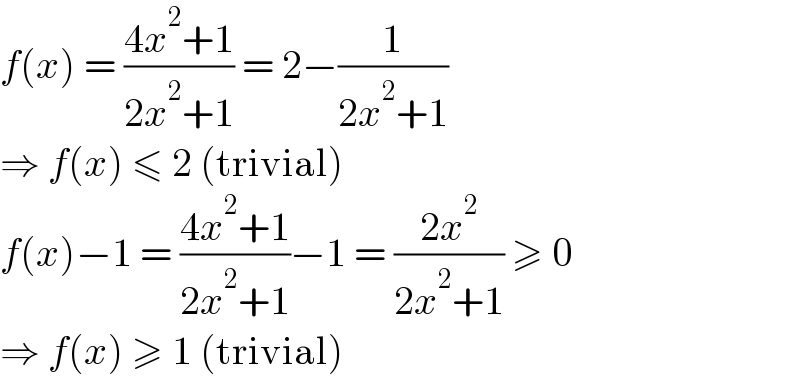
f(x) = ((4x^2 +1)/(2x^2 +1)) = 2−(1/(2x^2 +1)) ⇒ f(x) ≤ 2 (trivial) f(x)−1 = ((4x^2 +1)/(2x^2 +1))−1 = ((2x^2 )/(2x^2 +1)) ≥ 0 ⇒ f(x) ≥ 1 (trivial)

$${f}\left({x}\right)\:=\:\frac{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\:{f}\left({x}\right)\:\leqslant\:\mathrm{2}\:\left(\mathrm{trivial}\right) \\ $$$${f}\left({x}\right)−\mathrm{1}\:=\:\frac{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{1}\:=\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\:{f}\left({x}\right)\:\geqslant\:\mathrm{1}\:\left(\mathrm{trivial}\right) \\ $$

Answered by john_santu last updated on 25/Jan/21

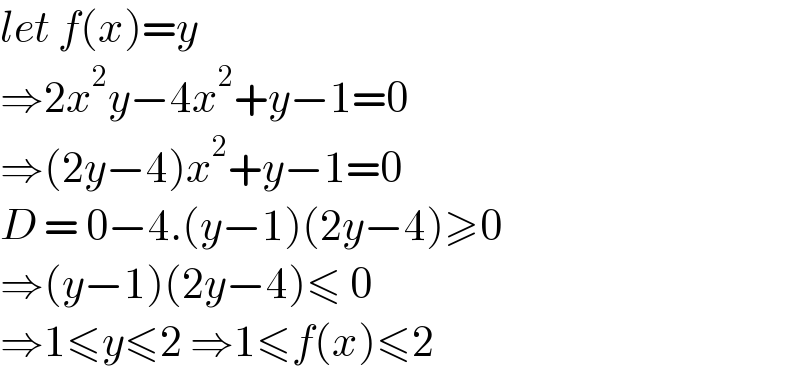
let f(x)=y ⇒2x^2 y−4x^2 +y−1=0 ⇒(2y−4)x^2 +y−1=0 D = 0−4.(y−1)(2y−4)≥0 ⇒(y−1)(2y−4)≤ 0 ⇒1≤y≤2 ⇒1≤f(x)≤2

$${let}\:{f}\left({x}\right)={y} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} {y}−\mathrm{4}{x}^{\mathrm{2}} +{y}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{y}−\mathrm{4}\right){x}^{\mathrm{2}} +{y}−\mathrm{1}=\mathrm{0} \\ $$$${D}\:=\:\mathrm{0}−\mathrm{4}.\left({y}−\mathrm{1}\right)\left(\mathrm{2}{y}−\mathrm{4}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\left({y}−\mathrm{1}\right)\left(\mathrm{2}{y}−\mathrm{4}\right)\leqslant\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}\leqslant{y}\leqslant\mathrm{2}\:\Rightarrow\mathrm{1}\leqslant{f}\left({x}\right)\leqslant\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com