Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 214116 by Ayya last updated on 28/Nov/24

f(x)=((3x−5)/x^2 )

$${f}\left({x}\right)=\frac{\mathrm{3}{x}−\mathrm{5}}{{x}^{\mathrm{2}} } \\ $$

Answered by issac last updated on 28/Nov/24

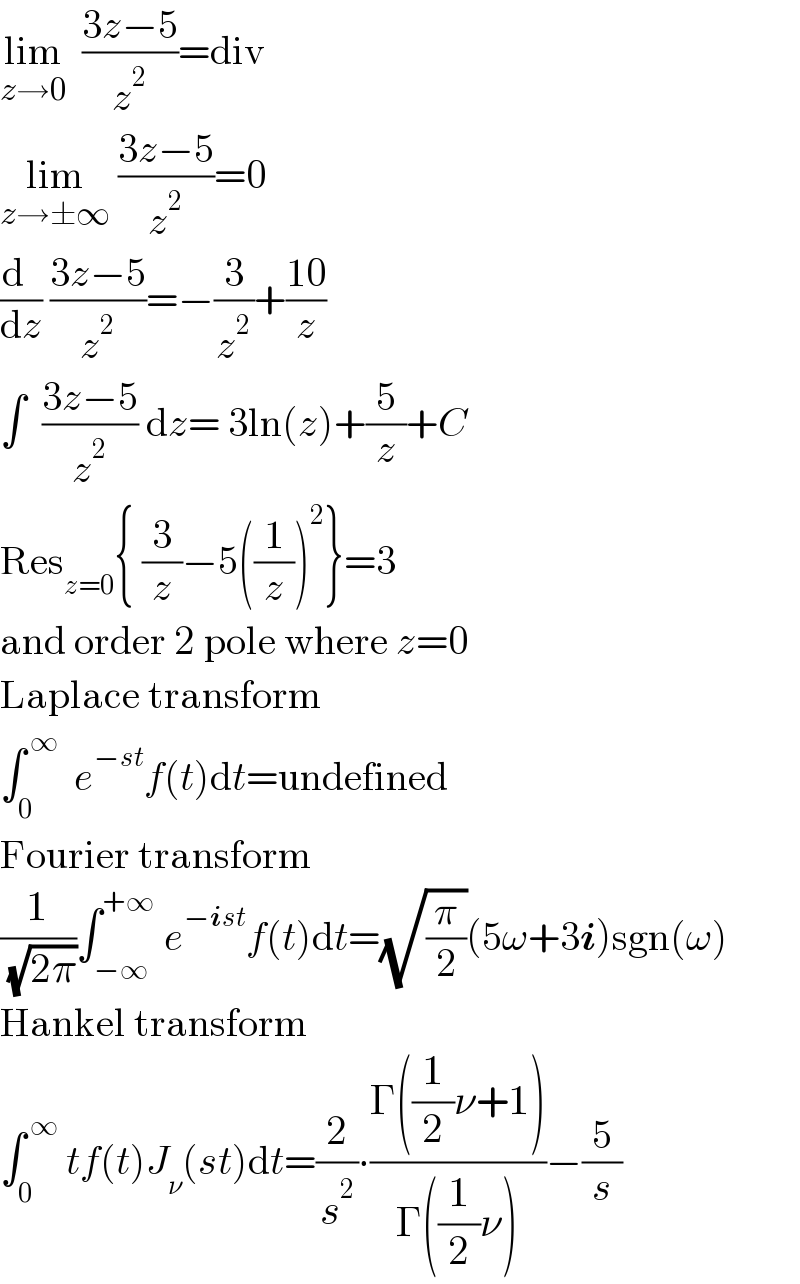
lim_(z→0) ((3z−5)/z^2 )=div lim_(z→±∞) ((3z−5)/z^2 )=0 ((d )/dz) ((3z−5)/z^2 )=−(3/z^2 )+((10)/z) ∫ ((3z−5)/z^2 ) dz= 3ln(z)+(5/z)+C Res_(z=0) { (3/z)−5((1/z))^2 }=3 and order 2 pole where z=0 Laplace transform ∫_0 ^( ∞) e^(−st) f(t)dt=undefined Fourier transform (1/( (√(2π))))∫_(−∞) ^(+∞) e^(−ist) f(t)dt=(√(π/2))(5ω+3i)sgn(ω) Hankel transform ∫_0 ^( ∞) tf(t)J_ν (st)dt=(2/s^2 )∙((Γ((1/2)ν+1))/(Γ((1/2)ν)))−(5/s)

$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{3}{z}−\mathrm{5}}{{z}^{\mathrm{2}} }=\mathrm{div} \\ $$$$\underset{{z}\rightarrow\pm\infty} {\mathrm{lim}}\:\frac{\mathrm{3}{z}−\mathrm{5}}{{z}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\mathrm{d}\:\:}{\mathrm{d}{z}}\:\frac{\mathrm{3}{z}−\mathrm{5}}{{z}^{\mathrm{2}} }=−\frac{\mathrm{3}}{{z}^{\mathrm{2}} }+\frac{\mathrm{10}}{{z}} \\ $$$$\int\:\:\frac{\mathrm{3}{z}−\mathrm{5}}{{z}^{\mathrm{2}} }\:\mathrm{d}{z}=\:\mathrm{3ln}\left({z}\right)+\frac{\mathrm{5}}{{z}}+{C} \\ $$$$\mathrm{Res}_{{z}=\mathrm{0}} \left\{\:\frac{\mathrm{3}}{{z}}−\mathrm{5}\left(\frac{\mathrm{1}}{{z}}\right)^{\mathrm{2}} \right\}=\mathrm{3}\: \\ $$$$\mathrm{and}\:\mathrm{order}\:\mathrm{2}\:\mathrm{pole}\:\mathrm{where}\:{z}=\mathrm{0} \\ $$$$\mathrm{Laplace}\:\mathrm{transform} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:\:{e}^{−{st}} {f}\left({t}\right)\mathrm{d}{t}=\mathrm{undefined} \\ $$$$\mathrm{Fourier}\:\mathrm{transform} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\int_{−\infty} ^{+\infty} \:{e}^{−\boldsymbol{{i}}{st}} {f}\left({t}\right)\mathrm{d}{t}=\sqrt{\frac{\pi}{\mathrm{2}}}\left(\mathrm{5}\omega+\mathrm{3}\boldsymbol{{i}}\right)\mathrm{sgn}\left(\omega\right) \\ $$$$\mathrm{Hankel}\:\mathrm{transform} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:{tf}\left({t}\right){J}_{\nu} \left({st}\right)\mathrm{d}{t}=\frac{\mathrm{2}}{{s}^{\mathrm{2}} }\centerdot\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\nu+\mathrm{1}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\nu\right)}−\frac{\mathrm{5}}{{s}} \\ $$

Answered by MathematicalUser2357 last updated on 20/Dec/24

$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com