
Question Number 39144 by Rio Mike last updated on 03/Jul/18
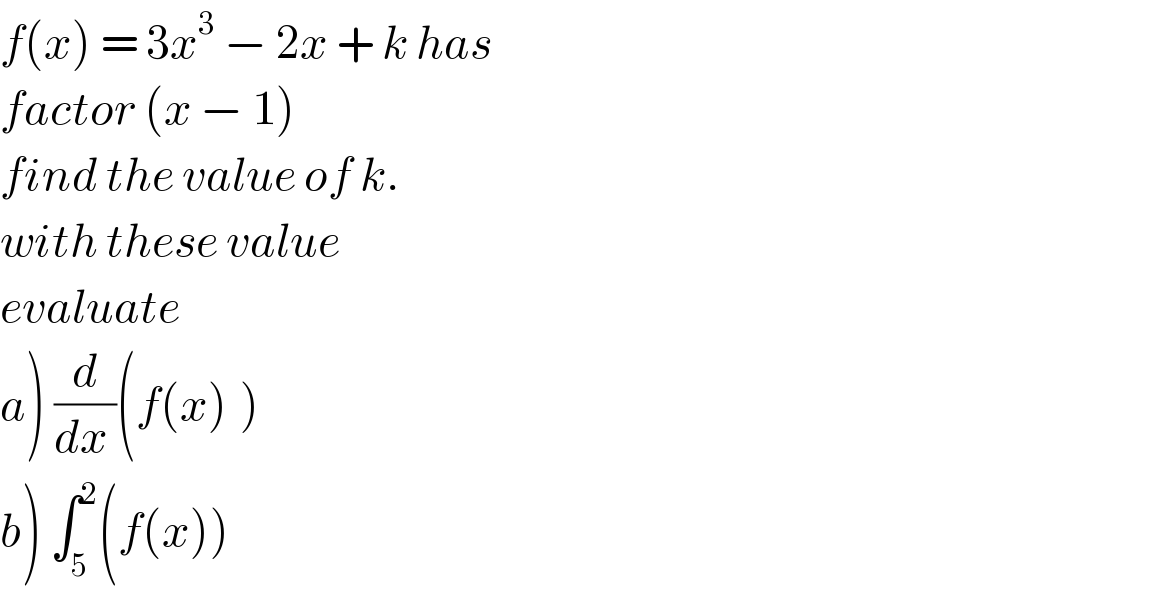
$${f}\left({x}\right)\:=\:\mathrm{3}{x}^{\mathrm{3}} \:−\:\mathrm{2}{x}\:+\:{k}\:{has}\: \\ $$$${factor}\:\left({x}\:−\:\mathrm{1}\right)\:\: \\ $$$${find}\:{the}\:{value}\:{of}\:{k}. \\ $$$${with}\:{these}\:{value}\: \\ $$$${evaluate} \\ $$$$\left.{a}\right)\:\frac{{d}}{{dx}\:}\left({f}\left({x}\right)_{} \right) \\ $$$$\left.{b}\right)\:\int_{\mathrm{5}} ^{\mathrm{2}} \left({f}\left({x}\right)\right) \\ $$
Answered by MJS last updated on 03/Jul/18
![(a) (d/dx)[f(x)]=f′(x)=9x^2 −2 (x−1)(x−α)(x−β)−(x^3 −(2/3)x+(k/3))=0 α+β+1=0 α+αβ+β+(2/3)=0 αβ+(k/3)=0 α=−β−1 β^2 +β+(1/3)=0 β^2 +β−(k/3)=0 ⇒ k=−1 f(x)=3x^3 −2x−1 (b) ∫_5 ^2 (3x^3 −2x−1)dx=[(3/4)x^4 −x^2 −x]_5 ^2 = =6−((1755)/4)=−((1731)/4)](Q39151.png)
$$\left({a}\right)\:\frac{{d}}{{dx}}\left[{f}\left({x}\right)\right]={f}'\left({x}\right)=\mathrm{9}{x}^{\mathrm{2}} −\mathrm{2} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−\alpha\right)\left({x}−\beta\right)−\left({x}^{\mathrm{3}} −\frac{\mathrm{2}}{\mathrm{3}}{x}+\frac{{k}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\alpha+\beta+\mathrm{1}=\mathrm{0} \\ $$$$\alpha+\alpha\beta+\beta+\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{0} \\ $$$$\alpha\beta+\frac{{k}}{\mathrm{3}}=\mathrm{0} \\ $$$$ \\ $$$$\alpha=−\beta−\mathrm{1} \\ $$$$\beta^{\mathrm{2}} +\beta+\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0} \\ $$$$\beta^{\mathrm{2}} +\beta−\frac{{k}}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\:{k}=−\mathrm{1} \\ $$$${f}\left({x}\right)=\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}{x}−\mathrm{1} \\ $$$$ \\ $$$$\left({b}\right)\:\underset{\mathrm{5}} {\overset{\mathrm{2}} {\int}}\left(\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}{x}−\mathrm{1}\right){dx}=\left[\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −{x}\right]_{\mathrm{5}} ^{\mathrm{2}} = \\ $$$$\:\:\:\:\:=\mathrm{6}−\frac{\mathrm{1755}}{\mathrm{4}}=−\frac{\mathrm{1731}}{\mathrm{4}} \\ $$
