
Question Number 130362 by greg_ed last updated on 24/Jan/21
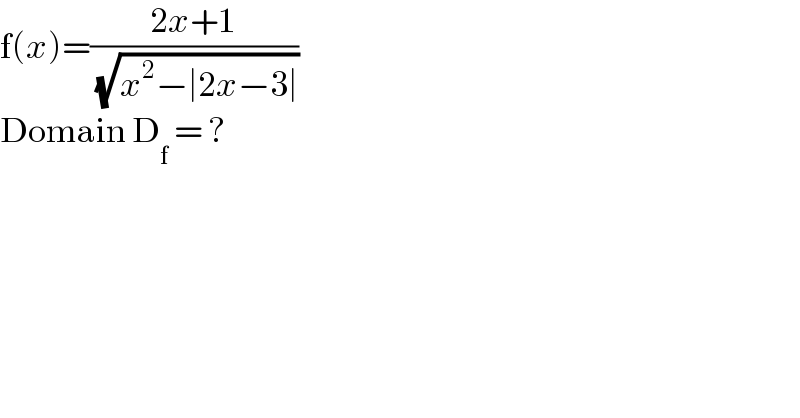
$$\mathrm{f}\left({x}\right)=\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mid\mathrm{2}{x}−\mathrm{3}\mid}} \\ $$$$\mathrm{Domain}\:\mathrm{D}_{\mathrm{f}} \:=\:? \\ $$
Answered by ajfour last updated on 24/Jan/21
![x^2 >∣2x−3∣ let x≥(3/2) & x^2 −2x+3>0 ⇒ (x−1)^2 +2 >0 ⇒ x∈[(3/2),∞) and if x<(3/2) x^2 +2x−3 > 0 (x+1)^2 >4 x<−3 or x> 1 ⇒ x∈(−∞,−3)∪(1,(3/2)) ⇒ x∈R−[−3,1]](Q130364.png)
$${x}^{\mathrm{2}} >\mid\mathrm{2}{x}−\mathrm{3}\mid \\ $$$${let}\:\:{x}\geqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\&\:\:\:\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}>\mathrm{0} \\ $$$$\Rightarrow\:\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\:>\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}\in\left[\frac{\mathrm{3}}{\mathrm{2}},\infty\right)\:\:\:\:\: \\ $$$${and}\:{if}\:{x}<\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}\:>\:\mathrm{0} \\ $$$$\:\:\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} >\mathrm{4} \\ $$$$\:\:\:\:\:{x}<−\mathrm{3}\:{or}\:\:\:{x}>\:\mathrm{1} \\ $$$$\Rightarrow\:\:{x}\in\left(−\infty,−\mathrm{3}\right)\cup\left(\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\:{x}\in\mathbb{R}−\left[−\mathrm{3},\mathrm{1}\right] \\ $$
Answered by mathmax by abdo last updated on 24/Jan/21
![f(x)=((2x+1)/( (√(x^2 −∣2x−3∣)))) x −∞ (3/2) +∞ ∣2x−3∣ −2x+3 0 2x−3 f(x) ((2x+1)/( (√(x^2 +2x−3))))... ((2x+1)/( (√(x^2 −2x+3)))) case1 x<(3/2) ⇒f(x)=((2x+1)/( (√(x^2 +2x−3)))) x∈D_f ⇔x^2 +2x−3>0 ⇔x^2 +2x+1−4>0 ⇒(x+1)^2 −4>0 ⇒ (x+1−2)(x+1+2)>0 ⇒(x−1)(x+3)>0 ⇒x∈]−∞,−3[∪]1,+∞[ ⇒ D_f =]−∞,−3[∪]1,(3/2)[ case 2 x≥(3/2) ⇒f(x)=((2x+1)/( (√(x^2 −2x+3)))) x∈D_f ⇔ x^2 −2x+3>0 ⇒(x−1)^2 +2>0 ⇒D_f =[(3/2),+∞[](Q130372.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mid\mathrm{2x}−\mathrm{3}\mid}} \\ $$$$\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\mid\mathrm{2x}−\mathrm{3}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2x}+\mathrm{3}\:\:\mathrm{0}\:\:\:\mathrm{2x}−\mathrm{3} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{3}}}...\:\:\:\:\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}}} \\ $$$$\mathrm{case1}\:\mathrm{x}<\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}}} \\ $$$$\mathrm{x}\in\mathrm{D}_{\mathrm{f}} \:\Leftrightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{3}>\mathrm{0}\:\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}−\mathrm{4}>\mathrm{0}\:\Rightarrow\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}>\mathrm{0}\:\Rightarrow \\ $$$$\left.\left(\mathrm{x}+\mathrm{1}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}+\mathrm{2}\right)>\mathrm{0}\:\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)>\mathrm{0}\:\:\Rightarrow\mathrm{x}\in\right]−\infty,−\mathrm{3}\left[\cup\right]\mathrm{1},+\infty\left[\:\Rightarrow\right. \\ $$$$\left.\mathrm{D}_{\mathrm{f}} =\right]−\infty,−\mathrm{3}\left[\cup\right]\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\left[\right. \\ $$$$\mathrm{case}\:\mathrm{2}\:\:\mathrm{x}\geqslant\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}}} \\ $$$$\mathrm{x}\in\mathrm{D}_{\mathrm{f}} \:\Leftrightarrow\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}>\mathrm{0}\:\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}>\mathrm{0}\:\:\Rightarrow\mathrm{D}_{\mathrm{f}} =\left[\frac{\mathrm{3}}{\mathrm{2}},+\infty\left[\right.\right. \\ $$
Answered by MJS_new last updated on 25/Jan/21
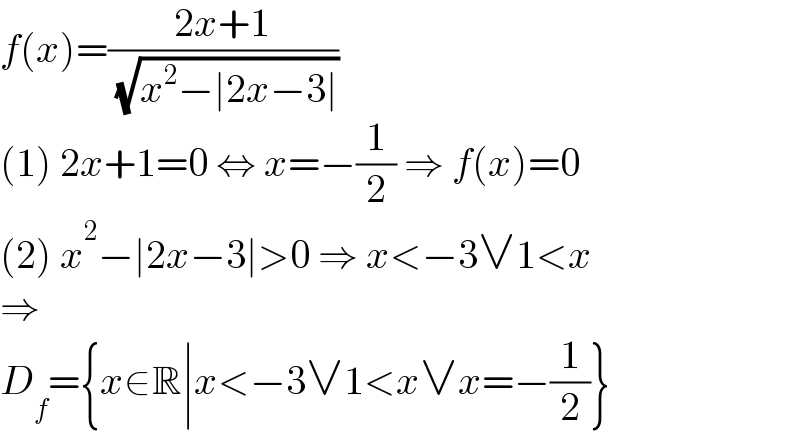
$${f}\left({x}\right)=\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mid\mathrm{2}{x}−\mathrm{3}\mid}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}{x}+\mathrm{1}=\mathrm{0}\:\Leftrightarrow\:{x}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{f}\left({x}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} −\mid\mathrm{2}{x}−\mathrm{3}\mid>\mathrm{0}\:\Rightarrow\:{x}<−\mathrm{3}\vee\mathrm{1}<{x} \\ $$$$\Rightarrow \\ $$$${D}_{{f}} =\left\{{x}\in\mathbb{R}\mid{x}<−\mathrm{3}\vee\mathrm{1}<{x}\vee{x}=−\frac{\mathrm{1}}{\mathrm{2}}\right\} \\ $$
