
Question Number 176850 by Ar Brandon last updated on 27/Sep/22
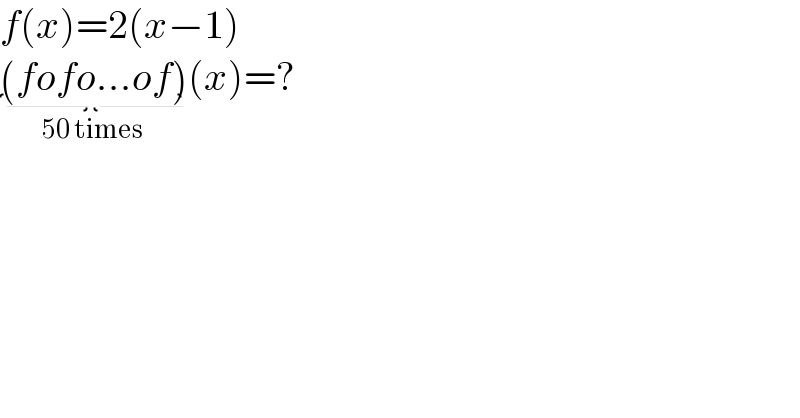
$${f}\left({x}\right)=\mathrm{2}\left({x}−\mathrm{1}\right) \\ $$$$\underset{\mathrm{50}\:\mathrm{times}} {\underbrace{\left({fofo}...{of}\right)}}\left({x}\right)=? \\ $$
Answered by mr W last updated on 27/Sep/22
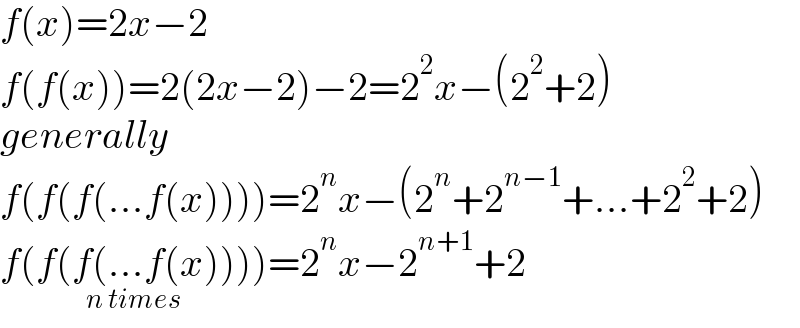
$${f}\left({x}\right)=\mathrm{2}{x}−\mathrm{2} \\ $$$${f}\left({f}\left({x}\right)\right)=\mathrm{2}\left(\mathrm{2}{x}−\mathrm{2}\right)−\mathrm{2}=\mathrm{2}^{\mathrm{2}} {x}−\left(\mathrm{2}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$${generally} \\ $$$${f}\left({f}\left({f}\left(...{f}\left({x}\right)\right)\right)\right)=\mathrm{2}^{{n}} {x}−\left(\mathrm{2}^{{n}} +\mathrm{2}^{{n}−\mathrm{1}} +...+\mathrm{2}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$$\underset{{n}\:{times}} {{f}\left({f}\left({f}\left(...{f}\left({x}\right)\right)\right)\right)}=\mathrm{2}^{{n}} {x}−\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{2} \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Thank you, Sir!
