Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 134204 by liberty last updated on 01/Mar/21

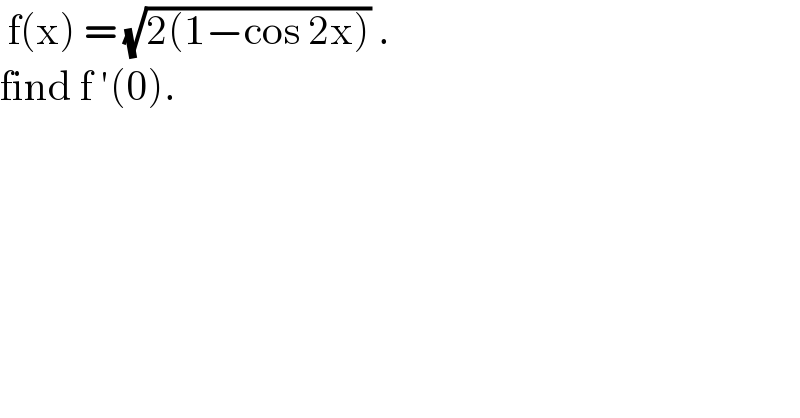
f(x) = (√(2(1−cos 2x))) . find f ′(0).

$$\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2x}\right)}\:. \\ $$$$\mathrm{find}\:\mathrm{f}\:'\left(\mathrm{0}\right). \\ $$

Answered by bramlexs22 last updated on 02/Mar/21

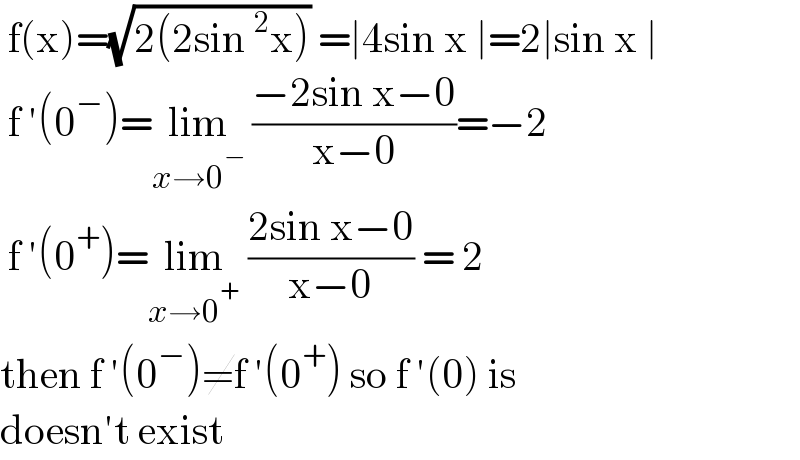
f(x)=(√(2(2sin^2 x))) =∣4sin x ∣=2∣sin x ∣ f ′(0^− )=lim_(x→0^− ) ((−2sin x−0)/(x−0))=−2 f ′(0^+ )=lim_(x→0^+ ) ((2sin x−0)/(x−0)) = 2 then f ′(0^− )≠f ′(0^+ ) so f ′(0) is doesn′t exist

$$\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{2}\left(\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)}\:=\mid\mathrm{4sin}\:\mathrm{x}\:\mid=\mathrm{2}\mid\mathrm{sin}\:\mathrm{x}\:\mid \\ $$$$\:\mathrm{f}\:'\left(\mathrm{0}^{−} \right)=\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{−\mathrm{2sin}\:\mathrm{x}−\mathrm{0}}{\mathrm{x}−\mathrm{0}}=−\mathrm{2}\: \\ $$$$\:\mathrm{f}\:'\left(\mathrm{0}^{+} \right)=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{2sin}\:\mathrm{x}−\mathrm{0}}{\mathrm{x}−\mathrm{0}}\:=\:\mathrm{2} \\ $$$$\mathrm{then}\:\mathrm{f}\:'\left(\mathrm{0}^{−} \right)\neq\mathrm{f}\:'\left(\mathrm{0}^{+} \right)\:\mathrm{so}\:\mathrm{f}\:'\left(\mathrm{0}\right)\:\mathrm{is}\: \\ $$$$\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com