
Previous in Relation and Functions Next in Relation and Functions
Question Number 57020 by 121194 last updated on 28/Mar/19
![[f(x+1)−f(x)]^2 =4[f(x)−1] f(x)=? −−−−−−−−−−−−− f(0)=0](Q57020.png)
$$\left[{f}\left({x}+\mathrm{1}\right)−{f}\left({x}\right)\right]^{\mathrm{2}} =\mathrm{4}\left[{f}\left({x}\right)−\mathrm{1}\right] \\ $$$${f}\left({x}\right)=? \\ $$$$−−−−−−−−−−−−− \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$
Commented by kaivan.ahmadi last updated on 28/Mar/19
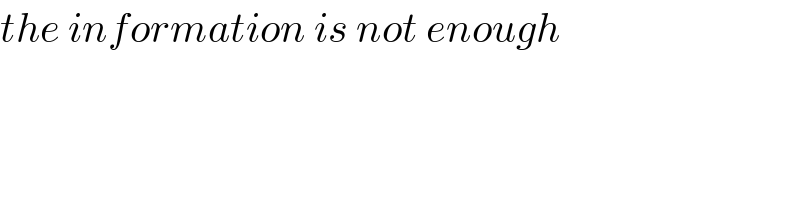
$${the}\:{information}\:{is}\:{not}\:{enough} \\ $$
Commented by kaivan.ahmadi last updated on 28/Mar/19
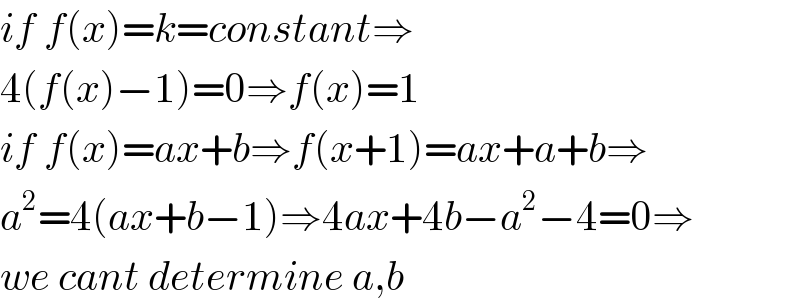
$${if}\:{f}\left({x}\right)={k}={constant}\Rightarrow \\ $$$$\mathrm{4}\left({f}\left({x}\right)−\mathrm{1}\right)=\mathrm{0}\Rightarrow{f}\left({x}\right)=\mathrm{1} \\ $$$${if}\:{f}\left({x}\right)={ax}+{b}\Rightarrow{f}\left({x}+\mathrm{1}\right)={ax}+{a}+{b}\Rightarrow \\ $$$${a}^{\mathrm{2}} =\mathrm{4}\left({ax}+{b}−\mathrm{1}\right)\Rightarrow\mathrm{4}{ax}+\mathrm{4}{b}−{a}^{\mathrm{2}} −\mathrm{4}=\mathrm{0}\Rightarrow \\ $$$${we}\:{cant}\:{determine}\:{a},{b} \\ $$
Commented by prakash jain last updated on 29/Mar/19

$${x}=\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)^{\mathrm{2}} =−\mathrm{4}\Rightarrow\mathrm{no}\:\mathrm{such}\:\mathrm{function}\:\mathrm{exists} \\ $$
