
Question Number 39440 by rahul 19 last updated on 06/Jul/18
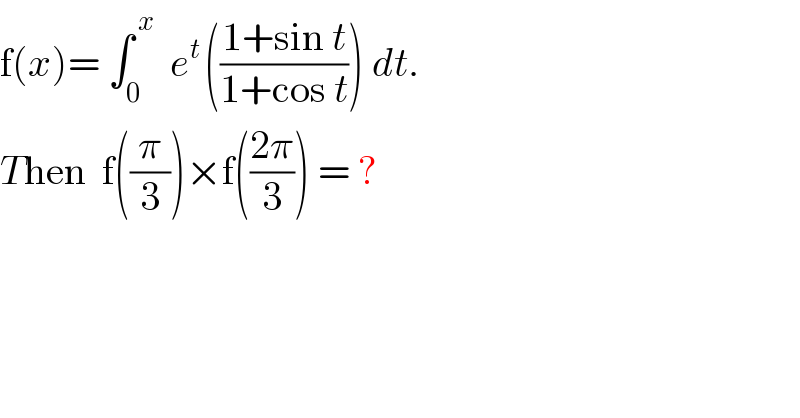
$$\mathrm{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\:{x}_{} } \:{e}^{{t}\:} \left(\frac{\mathrm{1}+\mathrm{sin}\:{t}}{\mathrm{1}+\mathrm{cos}\:{t}}\right)\:{dt}. \\ $$$${T}\mathrm{hen}\:\:\mathrm{f}\left(\frac{\pi}{\mathrm{3}}\right)×\mathrm{f}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:=\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18
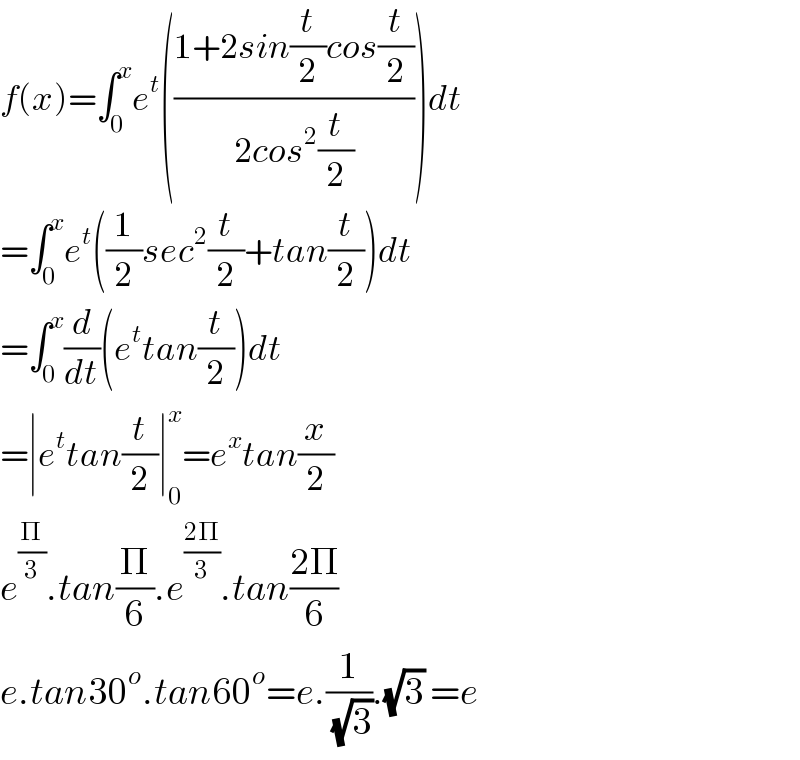
$${f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} {e}^{{t}} \left(\frac{\mathrm{1}+\mathrm{2}{sin}\frac{{t}}{\mathrm{2}}{cos}\frac{{t}}{\mathrm{2}}}{\mathrm{2}{cos}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{{x}} {e}^{{t}} \left(\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \frac{{t}}{\mathrm{2}}+{tan}\frac{{t}}{\mathrm{2}}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{{x}} \frac{{d}}{{dt}}\left({e}^{{t}} {tan}\frac{{t}}{\mathrm{2}}\right){dt} \\ $$$$=\mid{e}^{{t}} {tan}\frac{{t}}{\mathrm{2}}\mid_{\mathrm{0}} ^{{x}} ={e}^{{x}} {tan}\frac{{x}}{\mathrm{2}} \\ $$$${e}^{\frac{\Pi}{\mathrm{3}}} .{tan}\frac{\Pi}{\mathrm{6}}.{e}^{\frac{\mathrm{2}\Pi}{\mathrm{3}}} .{tan}\frac{\mathrm{2}\Pi}{\mathrm{6}} \\ $$$${e}.{tan}\mathrm{30}^{{o}} .{tan}\mathrm{60}^{{o}} ={e}.\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}.\sqrt{\mathrm{3}}\:={e} \\ $$
Commented by rahul 19 last updated on 06/Jul/18
Thank you sir . ����
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18
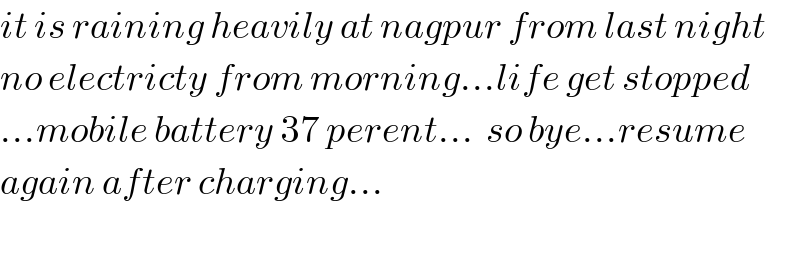
$${it}\:{is}\:{raining}\:{heavily}\:{at}\:{nagpur}\:{from}\:{last}\:{night} \\ $$$${no}\:{electricty}\:{from}\:{morning}...{life}\:{get}\:{stopped} \\ $$$$...{mobile}\:{battery}\:\mathrm{37}\:{perent}...\:\:{so}\:{bye}...{resume} \\ $$$${again}\:{after}\:{charging}... \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 06/Jul/18
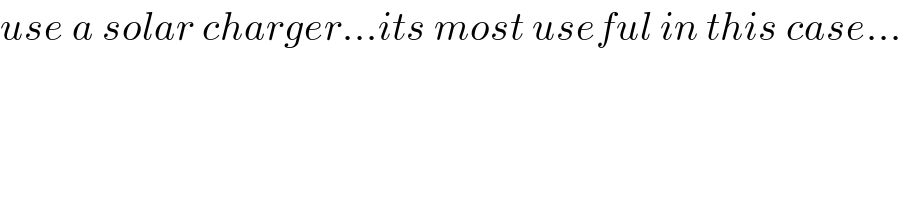
$${use}\:{a}\:{solar}\:{charger}...{its}\:{most}\:{useful}\:{in}\:{this}\:{case}... \\ $$
