
Question Number 1821 by 123456 last updated on 05/Oct/15
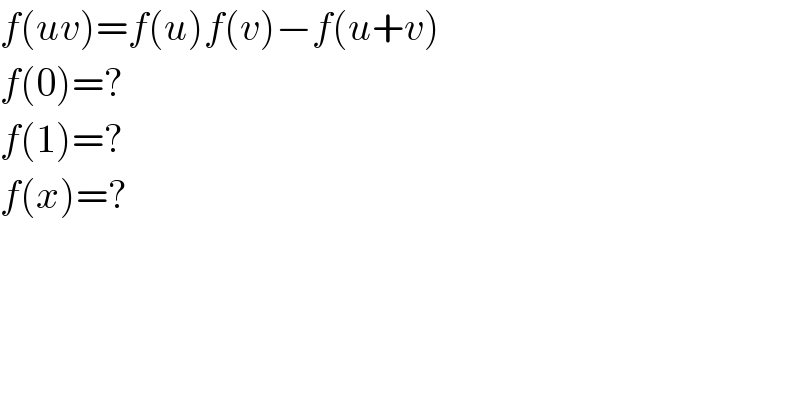
$${f}\left({uv}\right)={f}\left({u}\right){f}\left({v}\right)−{f}\left({u}+{v}\right) \\ $$$${f}\left(\mathrm{0}\right)=? \\ $$$${f}\left(\mathrm{1}\right)=? \\ $$$${f}\left({x}\right)=? \\ $$
Answered by Rasheed Soomro last updated on 10/Oct/15
![f(uv)=f(u)f(v)−f(u+v) Let u=0 and v=0 f(0.0)=f(0)f(0)−f(0+0) f(0)=[f(0)]^2 −f(0) [f(0)]^2 −2f(0)=0 f(0)[f(0)−2]=0 f(0)=0 Or f(0)=2...................(i) −−−−−−−−−−−−−−−−−−− Let u=1 and v=0 f(1.0)=f(1)f(0)−f(1+0) f(0)=f(1)[f(0)−1] f(1)=((f(0))/(f(0)−1))...........................(ii) When f(0)=0,f(1)=(0/(0−1))=0 When f(0)=2,f(1)=(2/(2−1))=2 f(1)=0 Or f(1)=2...........(iii) −−−−−−−−−−−−−−−−−− Let u=x and v=0 f(x.0)=f(x)f(0)−f(x+0) f(0)=f(x)[f(0)−1] f(x)=((f(0))/(f(0)−1)).................................(iv) When f(0)=0,f(x)=(0/(0−1))=0 When f(0)=2,f(x)=(2/(2−1))=2 f(x)=0 Or f(x)=2........................(v) −−−−−−−−−−−−−−−−−−−−− (i) , (iii) and (v) are answers. (v) is general definition of the function.](Q1833.png)
$${f}\left({uv}\right)={f}\left({u}\right){f}\left({v}\right)−{f}\left({u}+{v}\right) \\ $$$${Let}\:{u}=\mathrm{0}\:{and}\:{v}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}.\mathrm{0}\right)={f}\left(\mathrm{0}\right){f}\left(\mathrm{0}\right)−{f}\left(\mathrm{0}+\mathrm{0}\right) \\ $$$${f}\left(\mathrm{0}\right)=\left[{f}\left(\mathrm{0}\right)\right]^{\mathrm{2}} −{f}\left(\mathrm{0}\right) \\ $$$$\left[{f}\left(\mathrm{0}\right)\right]^{\mathrm{2}} −\mathrm{2}{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)\left[{f}\left(\mathrm{0}\right)−\mathrm{2}\right]=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\:\:{Or}\:{f}\left(\mathrm{0}\right)=\mathrm{2}...................\left({i}\right) \\ $$$$−−−−−−−−−−−−−−−−−−− \\ $$$${Let}\:{u}=\mathrm{1}\:\:{and}\:{v}=\mathrm{0} \\ $$$${f}\left(\mathrm{1}.\mathrm{0}\right)={f}\left(\mathrm{1}\right){f}\left(\mathrm{0}\right)−{f}\left(\mathrm{1}+\mathrm{0}\right) \\ $$$${f}\left(\mathrm{0}\right)={f}\left(\mathrm{1}\right)\left[{f}\left(\mathrm{0}\right)−\mathrm{1}\right] \\ $$$${f}\left(\mathrm{1}\right)=\frac{{f}\left(\mathrm{0}\right)}{{f}\left(\mathrm{0}\right)−\mathrm{1}}...........................\left({ii}\right) \\ $$$${When}\:{f}\left(\mathrm{0}\right)=\mathrm{0},{f}\left(\mathrm{1}\right)=\frac{\mathrm{0}}{\mathrm{0}−\mathrm{1}}=\mathrm{0} \\ $$$${When}\:{f}\left(\mathrm{0}\right)=\mathrm{2},{f}\left(\mathrm{1}\right)=\frac{\mathrm{2}}{\mathrm{2}−\mathrm{1}}=\mathrm{2} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0}\:\:\:{Or}\:{f}\left(\mathrm{1}\right)=\mathrm{2}...........\left({iii}\right) \\ $$$$−−−−−−−−−−−−−−−−−− \\ $$$${Let}\:{u}={x}\:{and}\:{v}=\mathrm{0} \\ $$$${f}\left({x}.\mathrm{0}\right)={f}\left({x}\right){f}\left(\mathrm{0}\right)−{f}\left({x}+\mathrm{0}\right) \\ $$$${f}\left(\mathrm{0}\right)={f}\left({x}\right)\left[{f}\left(\mathrm{0}\right)−\mathrm{1}\right] \\ $$$${f}\left({x}\right)=\frac{{f}\left(\mathrm{0}\right)}{{f}\left(\mathrm{0}\right)−\mathrm{1}}.................................\left({iv}\right) \\ $$$${When}\:{f}\left(\mathrm{0}\right)=\mathrm{0},{f}\left({x}\right)=\frac{\mathrm{0}}{\mathrm{0}−\mathrm{1}}=\mathrm{0} \\ $$$${When}\:{f}\left(\mathrm{0}\right)=\mathrm{2},{f}\left({x}\right)=\frac{\mathrm{2}}{\mathrm{2}−\mathrm{1}}=\mathrm{2} \\ $$$${f}\left({x}\right)=\mathrm{0}\:\:{Or}\:{f}\left({x}\right)=\mathrm{2}........................\left({v}\right) \\ $$$$−−−−−−−−−−−−−−−−−−−−− \\ $$$$\left({i}\right)\:,\:\left({iii}\right)\:{and}\:\:\left({v}\right)\:{are}\:{answers}. \\ $$$$\left({v}\right)\:{is}\:{general}\:{definition}\:{of}\:{the}\:{function}. \\ $$
