
Question Number 156128 by aaaspots last updated on 08/Oct/21

$$\:{f}:{X}\rightarrow{Y} \\ $$$${f}\left({E}\backslash{F}\right)={f}\left({E}\right)\backslash{f}\left({F}\right)\Rightarrow{f}\:{is}\:\mathrm{1}\:{to}\:\mathrm{1} \\ $$$$ \\ $$$${I}\:{think}\:{it}\:{is}\:{not}\:{true}\: \\ $$$${since}\:{let}\:{x}\mathrm{1}\:{x}\mathrm{2}\:{x}\mathrm{3}\in{E}\:,{x}\mathrm{3}\:{x}\mathrm{4}\in{F}, \\ $$$${and}\:{f}\left({x}\mathrm{1}\right)={f}\left(\:{x}\mathrm{2}\right)\:{it}\:{will}\:{be}\:{not}\:{true}. \\ $$$$ \\ $$$${but}\:{my}\:{friend}\:{say}\:{by}\:\sim{q}\Rightarrow\sim{p} \\ $$$$\:{f}\:{is}\:{not}\:\mathrm{1}\:{to}\:\mathrm{1} \\ $$$$\Rightarrow{f}\left({E}\backslash{F}\right)\neq{f}\left({E}\right)\backslash{f}\left({F}\right),{and}\:{take} \\ $$$${x}\mathrm{1}\:{x}\mathrm{2}\in{X},\:{f}\left({x}\mathrm{1}\right)={f}\left({x}\mathrm{2}\right)={y}\mathrm{0} \\ $$$${E}=\left\{{x}\mathrm{1}\:,{x}\mathrm{2}\right\}\:{F}=\left\{{x}\mathrm{2}\right\} \\ $$$${and}\:\:{can}\:{proof}\:{it}\:{is}\:{true} \\ $$$${but}\:{I}\:{do}\:{not}\:{know}\:{which}\:{is}\:{true} \\ $$$${how}\:{to}\:{proof}\:{it}? \\ $$
Answered by TheSupreme last updated on 08/Oct/21
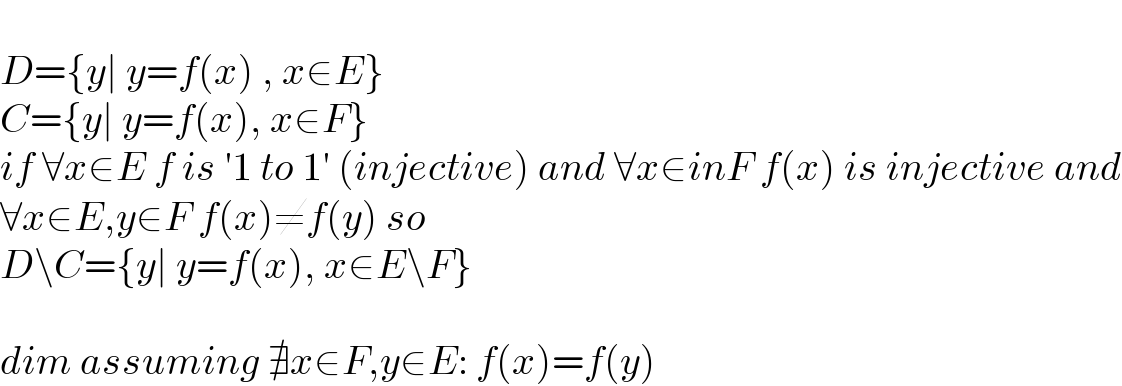
$$ \\ $$$${D}=\left\{{y}\mid\:{y}={f}\left({x}\right)\:,\:{x}\in{E}\right\} \\ $$$${C}=\left\{{y}\mid\:{y}={f}\left({x}\right),\:{x}\in{F}\right\} \\ $$$${if}\:\forall{x}\in{E}\:{f}\:{is}\:'\mathrm{1}\:{to}\:\mathrm{1}'\:\left({injective}\right)\:{and}\:\forall{x}\in{inF}\:{f}\left({x}\right)\:{is}\:{injective}\:{and} \\ $$$$\forall{x}\in{E},{y}\in{F}\:{f}\left({x}\right)\neq{f}\left({y}\right)\:{so} \\ $$$${D}\backslash{C}=\left\{{y}\mid\:{y}={f}\left({x}\right),\:{x}\in{E}\backslash{F}\right\} \\ $$$$ \\ $$$${dim}\:{assuming}\:\nexists{x}\in{F},{y}\in{E}:\:{f}\left({x}\right)={f}\left({y}\right)\: \\ $$
Commented by aaaspots last updated on 08/Oct/21
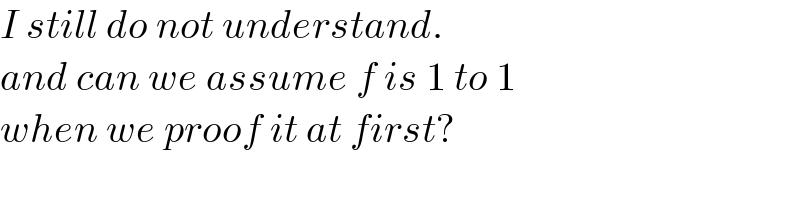
$${I}\:{still}\:{do}\:{not}\:{understand}. \\ $$$${and}\:{can}\:{we}\:{assume}\:{f}\:{is}\:\mathrm{1}\:{to}\:\mathrm{1}\: \\ $$$${when}\:{we}\:{proof}\:{it}\:{at}\:{first}? \\ $$$$ \\ $$
Commented by aaaspots last updated on 08/Oct/21
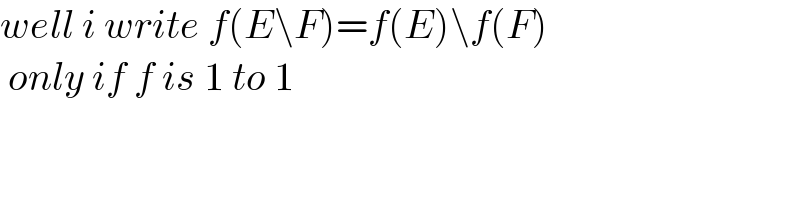
$${well}\:{i}\:{write}\:{f}\left({E}\backslash{F}\right)={f}\left({E}\right)\backslash{f}\left({F}\right)\: \\ $$$$\:{only}\:{if}\:{f}\:{is}\:\mathrm{1}\:{to}\:\mathrm{1} \\ $$
Commented by TheSupreme last updated on 08/Oct/21
![f(x) is 1 to 1 only if the proposition (1) is true for all E,F ∈ D[f(x)] D is dominium, prop 1 is your question](Q156163.png)
$${f}\left({x}\right)\:{is}\:\mathrm{1}\:{to}\:\mathrm{1}\:{only}\:{if}\:{the}\:{proposition}\:\left(\mathrm{1}\right)\:{is}\:{true}\:{for}\:{all}\:{E},{F}\:\in\:{D}\left[{f}\left({x}\right)\right] \\ $$$${D}\:{is}\:{dominium},\:{prop}\:\mathrm{1}\:{is}\:{your}\:{question} \\ $$
