Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217579 by Rasheed.Sindhi last updated on 16/Mar/25

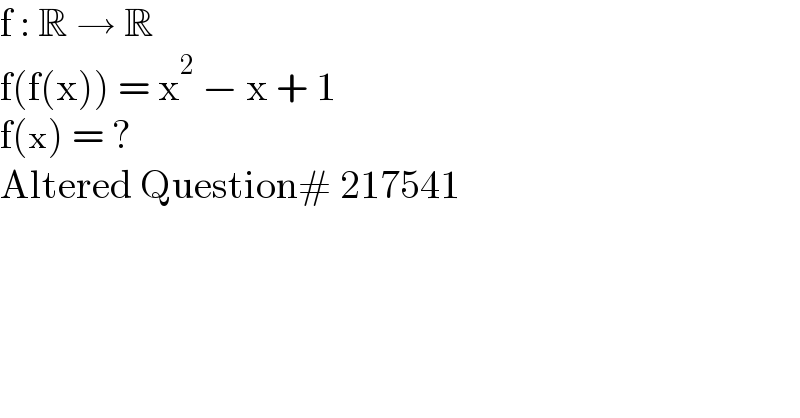
f : R → R f(f(x)) = x^2 − x + 1 f(x) = ? Altered Question# 217541

$$\mathrm{f}\::\:\mathbb{R}\:\rightarrow\:\mathbb{R} \\ $$$$\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{x}\:+\:\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:? \\ $$$$\mathrm{Altered}\:\mathrm{Question}#\:\mathrm{217541} \\ $$

Commented by Ghisom last updated on 16/Mar/25

I thought of this, there might be no closed term for f(x) because: g(g(x))=x^2 ⇒ g(x)=x^(√2) [not possible for x<0] but if we try to add terms: g(x)=x^(√2) +c ⇒ g(g(x))=(x^(√2) +c)^(√2) +c g(x)=x^(√2) +h(x) ⇒ weirdness

$$\mathrm{I}\:\mathrm{thought}\:\mathrm{of}\:\mathrm{this},\:\mathrm{there}\:\mathrm{might}\:\mathrm{be}\:\mathrm{no}\:\mathrm{closed} \\ $$$$\mathrm{term}\:\mathrm{for}\:{f}\left({x}\right) \\ $$$$\mathrm{because}: \\ $$$${g}\left({g}\left({x}\right)\right)={x}^{\mathrm{2}} \:\Rightarrow\:{g}\left({x}\right)={x}^{\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\:\left[\mathrm{not}\:\mathrm{possible}\:\mathrm{for}\:{x}<\mathrm{0}\right] \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{we}\:\mathrm{try}\:\mathrm{to}\:\mathrm{add}\:\mathrm{terms}: \\ $$$${g}\left({x}\right)={x}^{\sqrt{\mathrm{2}}} +{c}\:\Rightarrow\:{g}\left({g}\left({x}\right)\right)=\left({x}^{\sqrt{\mathrm{2}}} +{c}\right)^{\sqrt{\mathrm{2}}} +{c} \\ $$$${g}\left({x}\right)={x}^{\sqrt{\mathrm{2}}} +{h}\left({x}\right)\:\Rightarrow\:\mathrm{weirdness} \\ $$

Commented by mr W last updated on 16/Mar/25

with given condition we can find f(0), f(1), but we can even not find f(2) etc., not to mention f(x) generally. i think.

$${with}\:{given}\:{condition}\:{we}\:{can}\:{find}\: \\ $$$${f}\left(\mathrm{0}\right),\:{f}\left(\mathrm{1}\right),\:\:{but}\:{we}\:{can}\:{even}\:{not}\:{find}\: \\ $$$${f}\left(\mathrm{2}\right)\:{etc}.,\:{not}\:{to}\:{mention}\:{f}\left({x}\right) \\ $$$${generally}.\:{i}\:{think}. \\ $$

Commented by Rasheed.Sindhi last updated on 16/Mar/25

Thanks sirs!

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{sirs}}! \\ $$

Commented by Ghisom last updated on 17/Mar/25

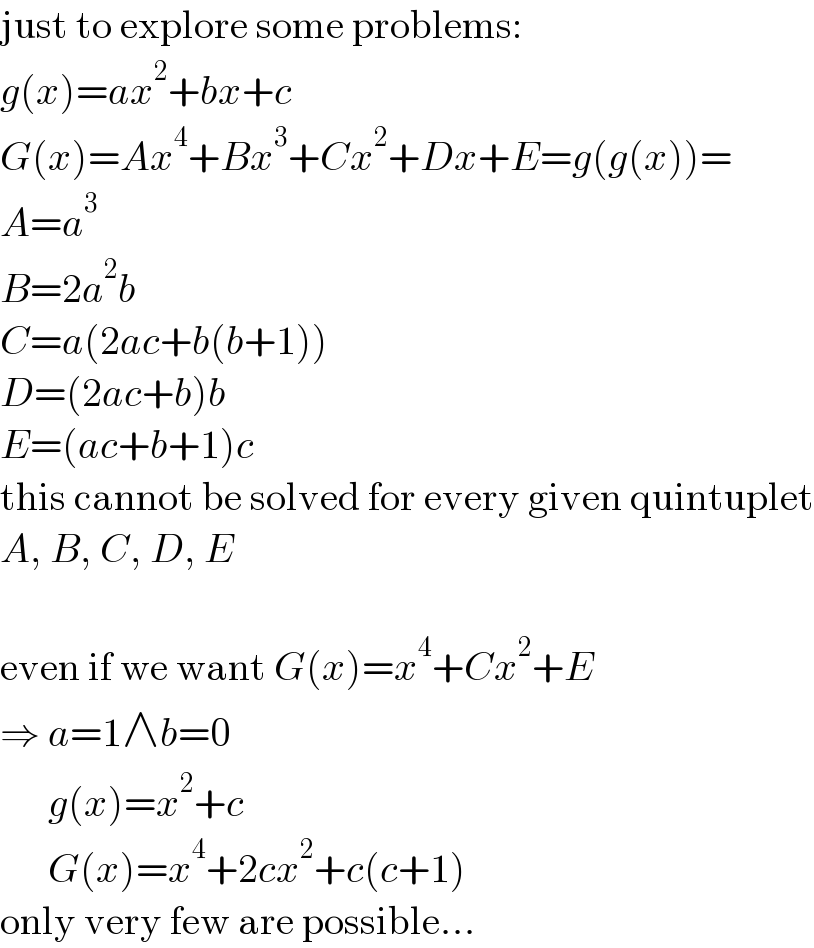
just to explore some problems: g(x)=ax^2 +bx+c G(x)=Ax^4 +Bx^3 +Cx^2 +Dx+E=g(g(x))= A=a^3 B=2a^2 b C=a(2ac+b(b+1)) D=(2ac+b)b E=(ac+b+1)c this cannot be solved for every given quintuplet A, B, C, D, E even if we want G(x)=x^4 +Cx^2 +E ⇒ a=1∧b=0 g(x)=x^2 +c G(x)=x^4 +2cx^2 +c(c+1) only very few are possible...

$$\mathrm{just}\:\mathrm{to}\:\mathrm{explore}\:\mathrm{some}\:\mathrm{problems}: \\ $$$${g}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${G}\left({x}\right)={Ax}^{\mathrm{4}} +{Bx}^{\mathrm{3}} +{Cx}^{\mathrm{2}} +{Dx}+{E}={g}\left({g}\left({x}\right)\right)= \\ $$$${A}={a}^{\mathrm{3}} \\ $$$${B}=\mathrm{2}{a}^{\mathrm{2}} {b} \\ $$$${C}={a}\left(\mathrm{2}{ac}+{b}\left({b}+\mathrm{1}\right)\right) \\ $$$${D}=\left(\mathrm{2}{ac}+{b}\right){b} \\ $$$${E}=\left({ac}+{b}+\mathrm{1}\right){c} \\ $$$$\mathrm{this}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:\mathrm{every}\:\mathrm{given}\:\mathrm{quintuplet} \\ $$$${A},\:{B},\:{C},\:{D},\:{E} \\ $$$$ \\ $$$$\mathrm{even}\:\mathrm{if}\:\mathrm{we}\:\mathrm{want}\:{G}\left({x}\right)={x}^{\mathrm{4}} +{Cx}^{\mathrm{2}} +{E} \\ $$$$\Rightarrow\:{a}=\mathrm{1}\wedge{b}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{g}\left({x}\right)={x}^{\mathrm{2}} +{c} \\ $$$$\:\:\:\:\:\:{G}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{2}{cx}^{\mathrm{2}} +{c}\left({c}+\mathrm{1}\right) \\ $$$$\mathrm{only}\:\mathrm{very}\:\mathrm{few}\:\mathrm{are}\:\mathrm{possible}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com