Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 37922 by gunawan last updated on 19/Jun/18

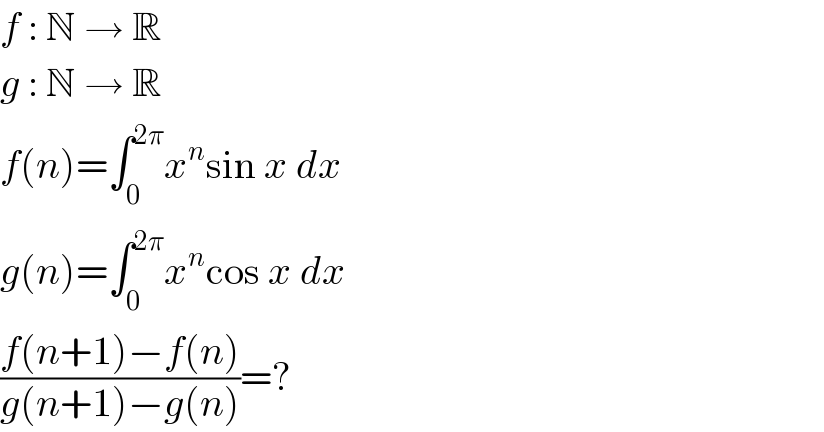
f : N → R g : N → R f(n)=∫_0 ^(2π) x^n sin x dx g(n)=∫_0 ^(2π) x^n cos x dx ((f(n+1)−f(n))/(g(n+1)−g(n)))=?

$${f}\::\:\mathbb{N}\:\rightarrow\:\mathbb{R} \\ $$$${g}\::\:\mathbb{N}\:\rightarrow\:\mathbb{R} \\ $$$${f}\left({n}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {x}^{{n}} \mathrm{sin}\:{x}\:{dx} \\ $$$${g}\left({n}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {x}^{{n}} \mathrm{cos}\:{x}\:{dx} \\ $$$$\frac{{f}\left({n}+\mathrm{1}\right)−{f}\left({n}\right)}{{g}\left({n}+\mathrm{1}\right)−{g}\left({n}\right)}=? \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Jun/18

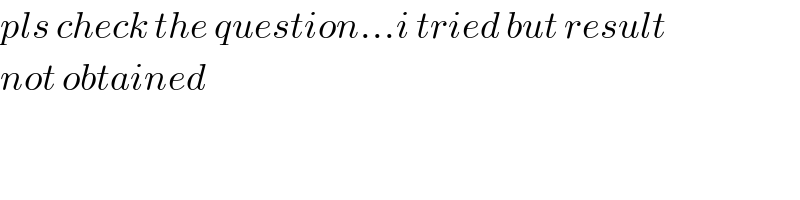
pls check the question...i tried but result not obtained

$${pls}\:{check}\:{the}\:{question}...{i}\:{tried}\:{but}\:{result} \\ $$$${not}\:{obtained} \\ $$

Commented by ajfour last updated on 20/Jun/18

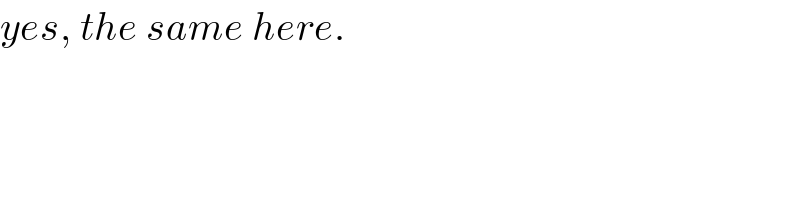
yes, the same here.

$${yes},\:{the}\:{same}\:{here}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jun/18

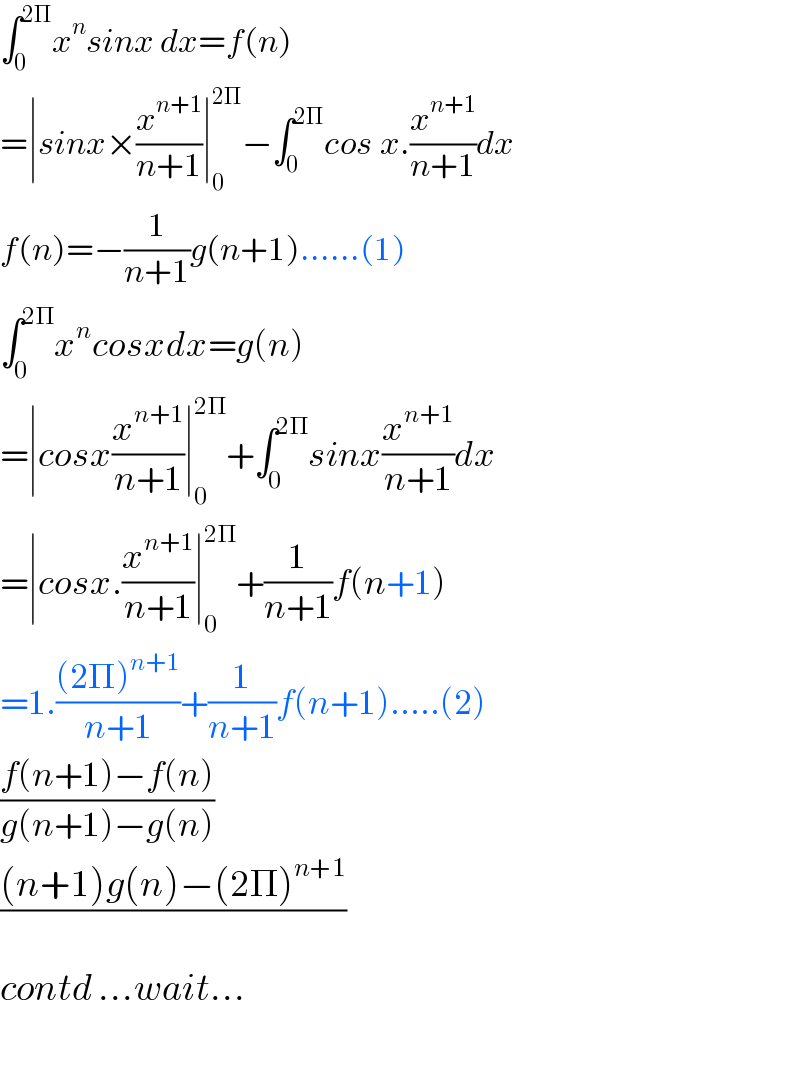
∫_0 ^(2Π) x^n sinx dx=f(n) =∣sinx×(x^(n+1) /(n+1))∣_0 ^(2Π) −∫_0 ^(2Π) cos^ x.(x^(n+1) /(n+1))dx f(n)=−(1/(n+1))g(n+1)......(1) ∫_0 ^(2Π) x^n cosxdx=g(n) =∣cosx(x^(n+1) /(n+1))∣_0 ^(2Π) +∫_0 ^(2Π) sinx(x^(n+1) /(n+1))dx =∣cosx.(x^(n+1) /(n+1))∣_0 ^(2Π) +(1/(n+1))f(n+1) =1.(((2Π)^(n+1) )/(n+1))+(1/(n+1))f(n+1).....(2) ((f(n+1)−f(n))/(g(n+1)−g(n))) (((n+1)g(n)−(2Π)^(n+1) )/) contd ...wait...

$$\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {x}^{{n}} {sinx}\:{dx}={f}\left({n}\right) \\ $$$$=\mid{sinx}×\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{2}\Pi} −\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {cos}^{} {x}.\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{dx} \\ $$$${f}\left({n}\right)=−\frac{\mathrm{1}}{{n}+\mathrm{1}}{g}\left({n}+\mathrm{1}\right)......\left(\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {x}^{{n}} {cosxdx}={g}\left({n}\right) \\ $$$$=\mid{cosx}\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{2}\Pi} +\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {sinx}\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{dx} \\ $$$$=\mid{cosx}.\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{2}\Pi} +\frac{\mathrm{1}}{{n}+\mathrm{1}}{f}\left({n}+\mathrm{1}\right) \\ $$$$=\mathrm{1}.\frac{\left(\mathrm{2}\Pi\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}{f}\left({n}+\mathrm{1}\right).....\left(\mathrm{2}\right) \\ $$$$\frac{{f}\left({n}+\mathrm{1}\right)−{f}\left({n}\right)}{{g}\left({n}+\mathrm{1}\right)−{g}\left({n}\right)} \\ $$$$\frac{\left({n}+\mathrm{1}\right){g}\left({n}\right)−\left(\mathrm{2}\Pi\right)^{{n}+\mathrm{1}} }{} \\ $$$${contd}\:...{wait}... \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com