
Question Number 151758 by mathdanisur last updated on 22/Aug/21
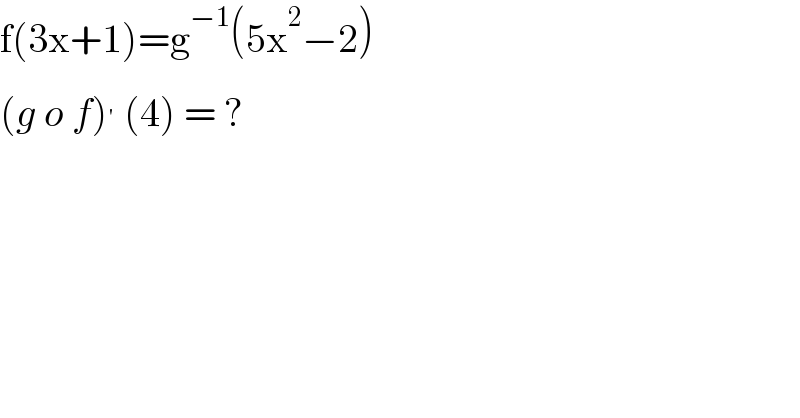
$$\mathrm{f}\left(\mathrm{3x}+\mathrm{1}\right)=\mathrm{g}^{−\mathrm{1}} \left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$$\left({g}\:{o}\:{f}\right)^{'} \:\left(\mathrm{4}\right)\:=\:? \\ $$
Commented by otchereabdullai@gmail.com last updated on 23/Aug/21

$$\mathrm{nice}! \\ $$
Answered by Olaf_Thorendsen last updated on 22/Aug/21
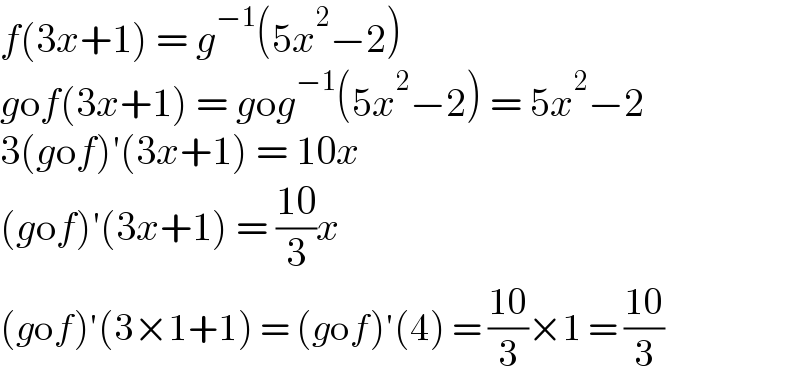
$${f}\left(\mathrm{3}{x}+\mathrm{1}\right)\:=\:{g}^{−\mathrm{1}} \left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$${g}\mathrm{o}{f}\left(\mathrm{3}{x}+\mathrm{1}\right)\:=\:{g}\mathrm{o}{g}^{−\mathrm{1}} \left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}\right)\:=\:\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{3}\left({g}\mathrm{o}{f}\right)'\left(\mathrm{3}{x}+\mathrm{1}\right)\:=\:\mathrm{10}{x} \\ $$$$\left({g}\mathrm{o}{f}\right)'\left(\mathrm{3}{x}+\mathrm{1}\right)\:=\:\frac{\mathrm{10}}{\mathrm{3}}{x} \\ $$$$\left({g}\mathrm{o}{f}\right)'\left(\mathrm{3}×\mathrm{1}+\mathrm{1}\right)\:=\:\left({g}\mathrm{o}{f}\right)'\left(\mathrm{4}\right)\:=\:\frac{\mathrm{10}}{\mathrm{3}}×\mathrm{1}\:=\:\frac{\mathrm{10}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 23/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Answered by mindispower last updated on 22/Aug/21
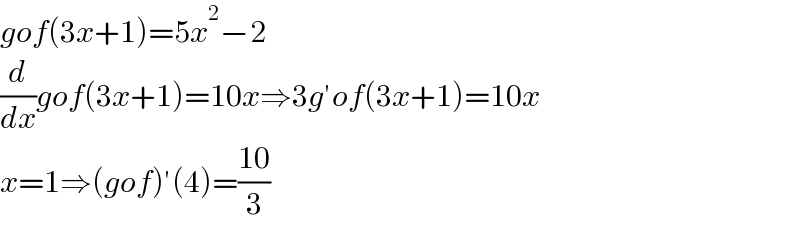
$${gof}\left(\mathrm{3}{x}+\mathrm{1}\right)=\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2} \\ $$$$\frac{{d}}{{dx}}{gof}\left(\mathrm{3}{x}+\mathrm{1}\right)=\mathrm{10}{x}\Rightarrow\mathrm{3}{g}'{of}\left(\mathrm{3}{x}+\mathrm{1}\right)=\mathrm{10}{x} \\ $$$${x}=\mathrm{1}\Rightarrow\left({gof}\right)'\left(\mathrm{4}\right)=\frac{\mathrm{10}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 23/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
