Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 206351 by MetaLahor1999 last updated on 12/Apr/24

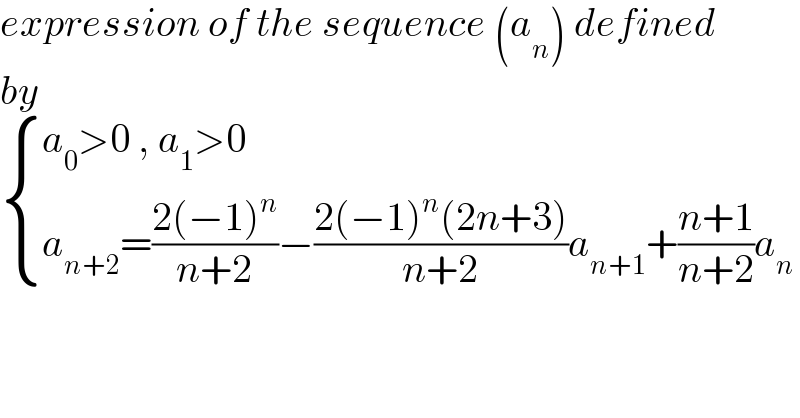
expression of the sequence (a_n ) defined by { ((a_0 >0 , a_1 >0)),((a_(n+2) =((2(−1)^n )/(n+2))−((2(−1)^n (2n+3))/(n+2))a_(n+1) +((n+1)/(n+2))a_n )) :}

$${expression}\:{of}\:{the}\:{sequence}\:\left({a}_{{n}} \right)\:{defined} \\ $$$${by}\: \\ $$$$\begin{cases}{{a}_{\mathrm{0}} >\mathrm{0}\:,\:{a}_{\mathrm{1}} >\mathrm{0}}\\{{a}_{{n}+\mathrm{2}} =\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{2}}−\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{2}{n}+\mathrm{3}\right)}{{n}+\mathrm{2}}{a}_{{n}+\mathrm{1}} +\frac{{n}+\mathrm{1}}{{n}+\mathrm{2}}{a}_{{n}} }\end{cases} \\ $$

Commented by TheHoneyCat last updated on 12/Apr/24

⇔ { ((a_0 >0 , a_1 >0)),((a_(n+2) =((2(−1)^n (1−2n−3))/(n+2))a_(n+1) +((n+1)/(n+2))a_n )) :} ⇔ { ((a_0 >0 , a_1 >0)),((a_(n+2) =((4(−1)^(n+1) (n+1))/(n+2))a_(n+1) +((n+1)/(n+2))a_n )) :} ⇔ { ((a_0 >0 , a_1 >0)),((a_(n+2) =((n+1)/(n+2))(4(−1)^(n+1) a_(n+1) +a_n ))) :} It is not a solution in any way... it′s just that I think this reformulation might make it easier... I might continue to work on it tomorow... good luck to anyone attempting.

$$\Leftrightarrow\begin{cases}{{a}_{\mathrm{0}} >\mathrm{0}\:,\:{a}_{\mathrm{1}} >\mathrm{0}}\\{{a}_{{n}+\mathrm{2}} =\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{1}−\mathrm{2}{n}−\mathrm{3}\right)}{{n}+\mathrm{2}}{a}_{{n}+\mathrm{1}} +\frac{{n}+\mathrm{1}}{{n}+\mathrm{2}}{a}_{{n}} }\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{{a}_{\mathrm{0}} >\mathrm{0}\:,\:{a}_{\mathrm{1}} >\mathrm{0}}\\{{a}_{{n}+\mathrm{2}} =\frac{\mathrm{4}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)}{{n}+\mathrm{2}}{a}_{{n}+\mathrm{1}} +\frac{{n}+\mathrm{1}}{{n}+\mathrm{2}}{a}_{{n}} }\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{{a}_{\mathrm{0}} >\mathrm{0}\:,\:{a}_{\mathrm{1}} >\mathrm{0}}\\{{a}_{{n}+\mathrm{2}} =\frac{{n}+\mathrm{1}}{{n}+\mathrm{2}}\left(\mathrm{4}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {a}_{{n}+\mathrm{1}} +{a}_{{n}} \right)}\end{cases} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{any}\:\mathrm{way}... \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{that}\:\mathrm{I}\:\mathrm{think}\:\mathrm{this}\:\mathrm{reformulation}\:\mathrm{might} \\ $$$$\mathrm{make}\:\mathrm{it}\:\mathrm{easier}... \\ $$$$\mathrm{I}\:\mathrm{might}\:\mathrm{continue}\:\mathrm{to}\:\mathrm{work}\:\mathrm{on}\:\mathrm{it}\:\mathrm{tomorow}... \\ $$$$\mathrm{good}\:\mathrm{luck}\:\mathrm{to}\:\mathrm{anyone}\:\mathrm{attempting}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com