Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 87245 by redmiiuser last updated on 03/Apr/20

expand (1+x)^(−1) using maclaurins theorem and talyors formula

$${expand}\: \\ $$$$\left(\mathrm{1}+{x}\right)^{−\mathrm{1}} \\ $$$${using}\:{maclaurins} \\ $$$${theorem}\:{and}\:{talyors} \\ $$$${formula} \\ $$

Commented by jagoll last updated on 03/Apr/20

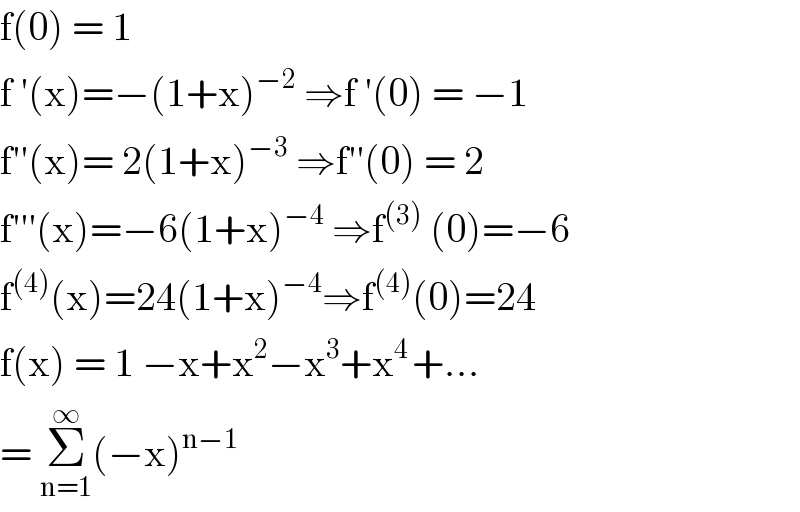
f(0) = 1 f ′(x)=−(1+x)^(−2) ⇒f ′(0) = −1 f′′(x)= 2(1+x)^(−3) ⇒f′′(0) = 2 f′′′(x)=−6(1+x)^(−4) ⇒f^((3)) (0)=−6 f^((4)) (x)=24(1+x)^(−4) ⇒f^((4)) (0)=24 f(x) = 1 −x+x^2 −x^3 +x^(4 ) +... = Σ_(n=1) ^∞ (−x)^(n−1)

$$\mathrm{f}\left(\mathrm{0}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=−\left(\mathrm{1}+\mathrm{x}\right)^{−\mathrm{2}} \:\Rightarrow\mathrm{f}\:'\left(\mathrm{0}\right)\:=\:−\mathrm{1} \\ $$$$\mathrm{f}''\left(\mathrm{x}\right)=\:\mathrm{2}\left(\mathrm{1}+\mathrm{x}\right)^{−\mathrm{3}} \:\Rightarrow\mathrm{f}''\left(\mathrm{0}\right)\:=\:\mathrm{2} \\ $$$$\mathrm{f}'''\left(\mathrm{x}\right)=−\mathrm{6}\left(\mathrm{1}+\mathrm{x}\right)^{−\mathrm{4}} \:\Rightarrow\mathrm{f}^{\left(\mathrm{3}\right)} \:\left(\mathrm{0}\right)=−\mathrm{6} \\ $$$$\mathrm{f}^{\left(\mathrm{4}\right)} \left(\mathrm{x}\right)=\mathrm{24}\left(\mathrm{1}+\mathrm{x}\right)^{−\mathrm{4}} \Rightarrow\mathrm{f}^{\left(\mathrm{4}\right)} \left(\mathrm{0}\right)=\mathrm{24} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{1}\:−\mathrm{x}+\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{4}\:} +... \\ $$$$=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \\ $$

Commented by jagoll last updated on 03/Apr/20

x ≠ −1

$$\mathrm{x}\:\neq\:−\mathrm{1} \\ $$

Commented by redmiiuser last updated on 03/Apr/20

ok mister i want to ask are there any conditions for the above expansion.

$${ok}\:{mister}\:{i}\:{want}\:{to}\:{ask} \\ $$$${are}\:{there}\:{any}\:{conditions} \\ $$$${for}\:{the}\:{above}\:{expansion}. \\ $$

Commented by jagoll last updated on 03/Apr/20

i think no sir

$$\mathrm{i}\:\mathrm{think}\:\mathrm{no}\:\mathrm{sir} \\ $$

Commented by redmiiuser last updated on 03/Apr/20

Are you 100% sure.

$${Are}\:{you}\:\mathrm{100\%}\:{sure}. \\ $$

Commented by Ar Brandon last updated on 03/Apr/20

∣x∣<1

$$\mid{x}\mid<\mathrm{1} \\ $$

Commented by redmiiuser last updated on 03/Apr/20

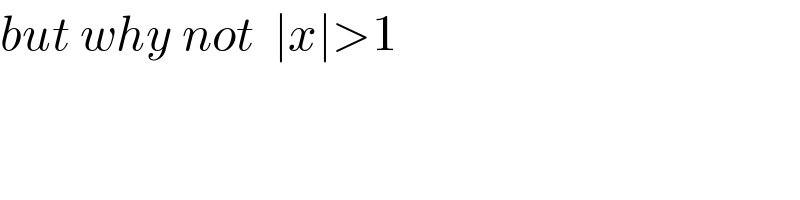
but why not ∣x∣>1

$${but}\:{why}\:{not}\:\:\mid{x}\mid>\mathrm{1} \\ $$

Commented by redmiiuser last updated on 03/Apr/20

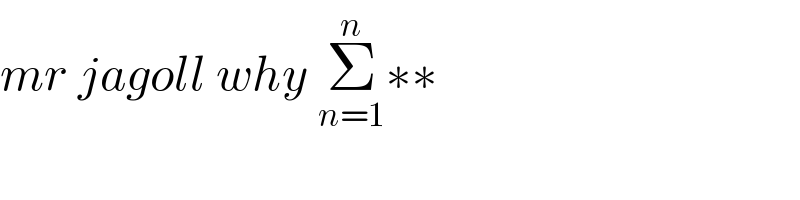
mr jagoll why Σ_(n=1) ^n ∗∗

$${mr}\:{jagoll}\:{why}\:\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\ast\ast \\ $$

Commented by jagoll last updated on 03/Apr/20

o yes it typo

$$\mathrm{o}\:\mathrm{yes}\:\mathrm{it}\:\mathrm{typo} \\ $$

Commented by redmiiuser last updated on 03/Apr/20

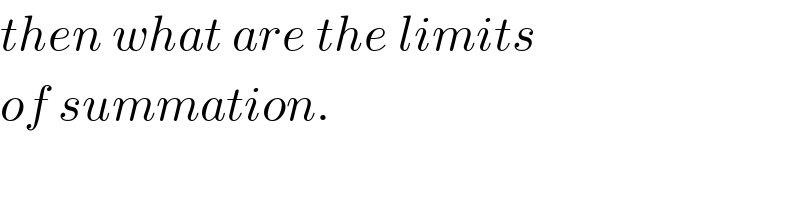
then what are the limits of summation.

$${then}\:{what}\:{are}\:{the}\:{limits} \\ $$$${of}\:{summation}. \\ $$

Commented by redmiiuser last updated on 03/Apr/20

cananyone comment

$${cananyone}\:{comment} \\ $$

Commented by Joel578 last updated on 03/Apr/20

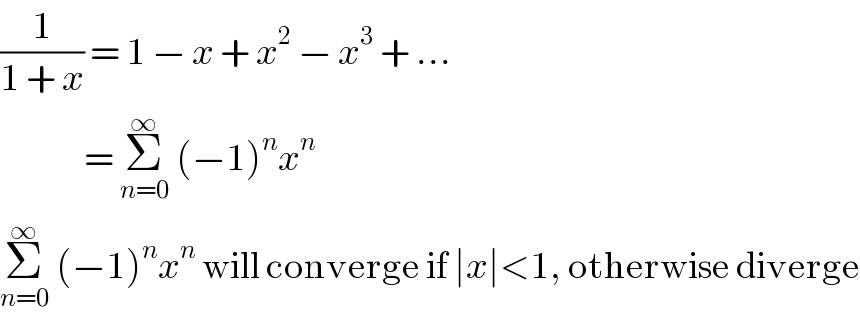
(1/(1 + x)) = 1 − x + x^2 − x^3 + ... = Σ_(n=0) ^∞ (−1)^n x^n Σ_(n=0) ^∞ (−1)^n x^n will converge if ∣x∣<1, otherwise diverge

$$\frac{\mathrm{1}}{\mathrm{1}\:+\:{x}}\:=\:\mathrm{1}\:−\:{x}\:+\:{x}^{\mathrm{2}} \:−\:{x}^{\mathrm{3}} \:+\:... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\: \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\mathrm{will}\:\mathrm{converge}\:\mathrm{if}\:\mid{x}\mid<\mathrm{1},\:\mathrm{otherwise}\:\mathrm{diverge} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com