Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 182786 by SANOGO last updated on 14/Dec/22

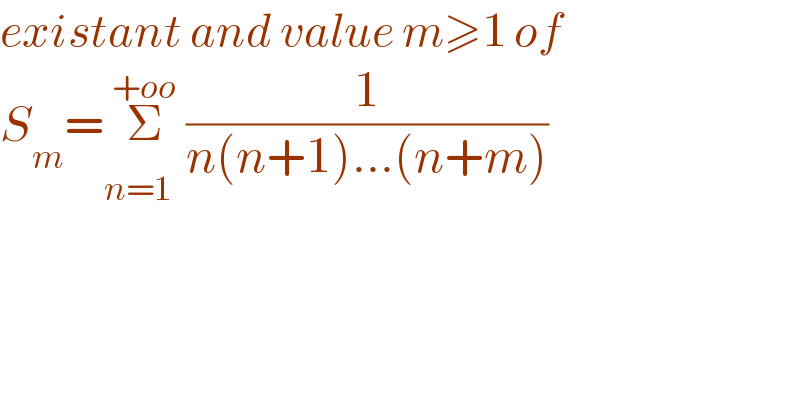
existant and value m≥1 of S_m =Σ_(n=1 ^ ) ^(+oo) (1/(n(n+1)...(n+m)))

$${existant}\:{and}\:{value}\:{m}\geqslant\mathrm{1}\:{of} \\ $$$${S}_{{m}} =\underset{{n}=\mathrm{1}\:\overset{} {\:}} {\overset{+{oo}} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)...\left({n}+{m}\right)}\: \\ $$

Answered by dre23 last updated on 15/Dec/22

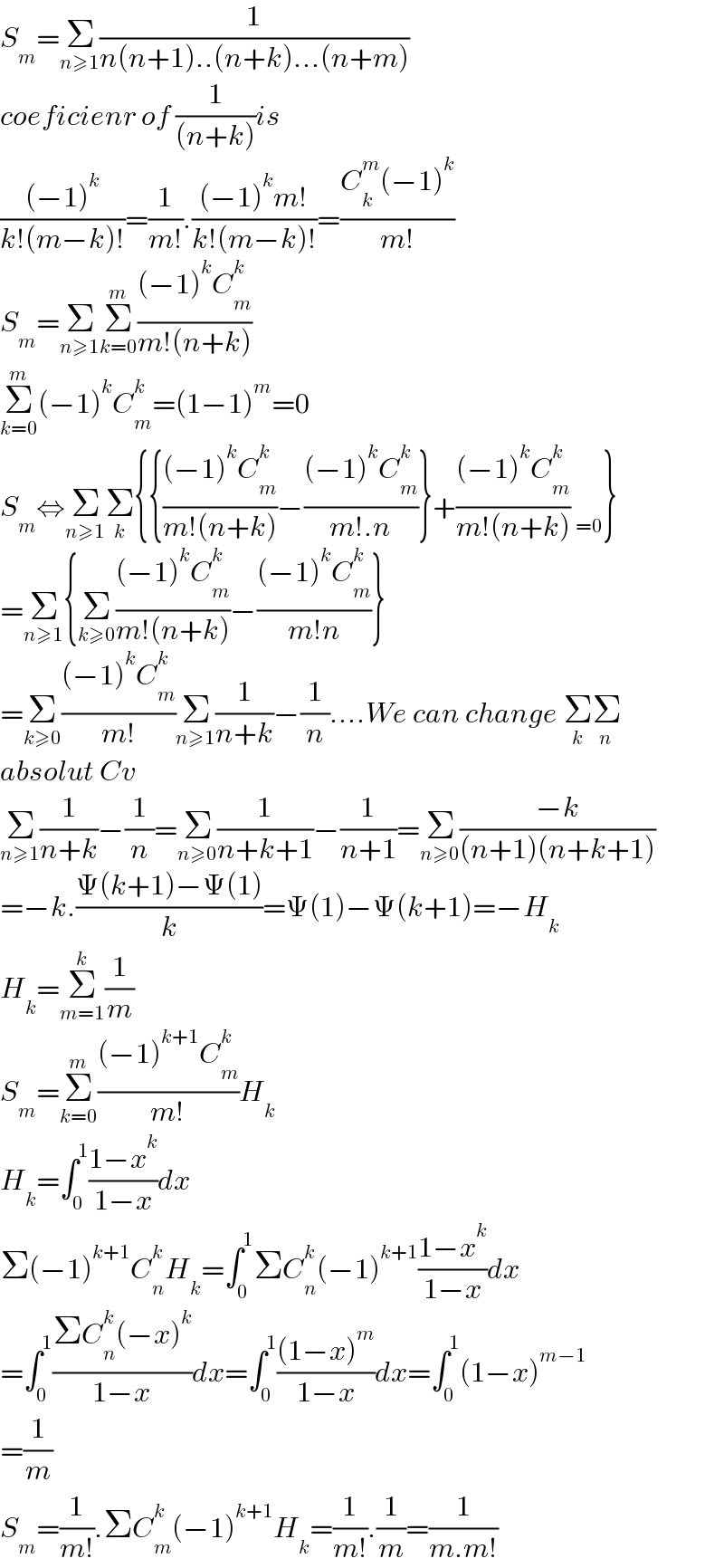
S_m =Σ_(n≥1) (1/(n(n+1)..(n+k)...(n+m))) coeficienr of (1/((n+k)))is (((−1)^k )/(k!(m−k)!))=(1/(m!)).(((−1)^k m!)/(k!(m−k)!))=((C_k ^m (−1)^k )/(m!)) S_m =Σ_(n≥1) Σ_(k=0) ^m (((−1)^k C_m ^k )/(m!(n+k))) Σ_(k=0) ^m (−1)^k C_m ^k =(1−1)^m =0 S_m ⇔Σ_(n≥1) Σ_k {{(((−1)^k C_m ^k )/(m!(n+k)))−(((−1)^k C_m ^k )/(m!.n))}+(((−1)^k C_m ^k )/(m!(n+k))) _(=0) } =Σ_(n≥1) {Σ_(k≥0) (((−1)^k C_m ^k )/(m!(n+k)))−(((−1)^k C_m ^k )/(m!n))} =Σ_(k≥0) (((−1)^k C_m ^k )/(m!))Σ_(n≥1) (1/(n+k))−(1/n)....We can change Σ_k Σ_n absolut Cv Σ_(n≥1) (1/(n+k))−(1/n)=Σ_(n≥0) (1/(n+k+1))−(1/(n+1))=Σ_(n≥0) ((−k)/((n+1)(n+k+1))) =−k.((Ψ(k+1)−Ψ(1))/k)=Ψ(1)−Ψ(k+1)=−H_k H_k =Σ_(m=1) ^k (1/m) S_m =Σ_(k=0) ^m (((−1)^(k+1) C_m ^k )/(m!))H_k H_k =∫_0 ^1 ((1−x^k )/(1−x))dx Σ(−1)^(k+1) C_n ^k H_k =∫_0 ^1 ΣC_n ^k (−1)^(k+1) ((1−x^k )/(1−x))dx =∫_0 ^1 ((ΣC_n ^k (−x)^k )/(1−x))dx=∫_0 ^1 (((1−x)^m )/(1−x))dx=∫_0 ^1 (1−x)^(m−1) =(1/m) S_m =(1/(m!)).ΣC_m ^k (−1)^(k+1) H_k =(1/(m!)).(1/m)=(1/(m.m!))

$${S}_{{m}} =\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)..\left({n}+{k}\right)...\left({n}+{m}\right)} \\ $$$${coeficienr}\:{of}\:\frac{\mathrm{1}}{\left({n}+{k}\right)}{is} \\ $$$$\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!\left({m}−{k}\right)!}=\frac{\mathrm{1}}{{m}!}.\frac{\left(−\mathrm{1}\right)^{{k}} {m}!}{{k}!\left({m}−{k}\right)!}=\frac{{C}_{{k}} ^{{m}} \left(−\mathrm{1}\right)^{{k}} }{{m}!} \\ $$$${S}_{{m}} =\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}=\mathrm{0}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} }{{m}!\left({n}+{k}\right)} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{m}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} =\left(\mathrm{1}−\mathrm{1}\right)^{{m}} =\mathrm{0} \\ $$$${S}_{{m}} \Leftrightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}} {\sum}\left\{\left\{\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} }{{m}!\left({n}+{k}\right)}−\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} }{{m}!.{n}}\right\}+\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} }{{m}!\left({n}+{k}\right)}\:_{=\mathrm{0}} \right\} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\left\{\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} }{{m}!\left({n}+{k}\right)}−\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} }{{m}!{n}}\right\} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{m}} ^{{k}} }{{m}!}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}+{k}}−\frac{\mathrm{1}}{{n}}....{We}\:{can}\:{change}\:\underset{{k}} {\sum}\underset{{n}} {\sum} \\ $$$${absolut}\:{Cv} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}+{k}}−\frac{\mathrm{1}}{{n}}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}+{k}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{−{k}}{\left({n}+\mathrm{1}\right)\left({n}+{k}+\mathrm{1}\right)} \\ $$$$=−{k}.\frac{\Psi\left({k}+\mathrm{1}\right)−\Psi\left(\mathrm{1}\right)}{{k}}=\Psi\left(\mathrm{1}\right)−\Psi\left({k}+\mathrm{1}\right)=−{H}_{{k}} \\ $$$${H}_{{k}} =\underset{{m}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{m}} \\ $$$${S}_{{m}} =\underset{{k}=\mathrm{0}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {C}_{{m}} ^{{k}} }{{m}!}{H}_{{k}} \\ $$$${H}_{{k}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{{k}} }{\mathrm{1}−{x}}{dx} \\ $$$$\Sigma\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {C}_{{n}} ^{{k}} {H}_{{k}} =\int_{\mathrm{0}} ^{\mathrm{1}} \Sigma{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \frac{\mathrm{1}−{x}^{{k}} }{\mathrm{1}−{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\Sigma{C}_{{n}} ^{{k}} \left(−{x}\right)^{{k}} }{\mathrm{1}−{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{{m}} }{\mathrm{1}−{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{m}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{m}} \\ $$$${S}_{{m}} =\frac{\mathrm{1}}{{m}!}.\Sigma{C}_{{m}} ^{{k}} \left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {H}_{{k}} =\frac{\mathrm{1}}{{m}!}.\frac{\mathrm{1}}{{m}}=\frac{\mathrm{1}}{{m}.{m}!} \\ $$

Commented by SANOGO last updated on 14/Dec/22

merci

$${merci} \\ $$

Commented by dre23 last updated on 16/Dec/22

je vous en prie

$${je}\:{vous}\:{en}\:{prie} \\ $$

Answered by mnjuly1970 last updated on 14/Dec/22

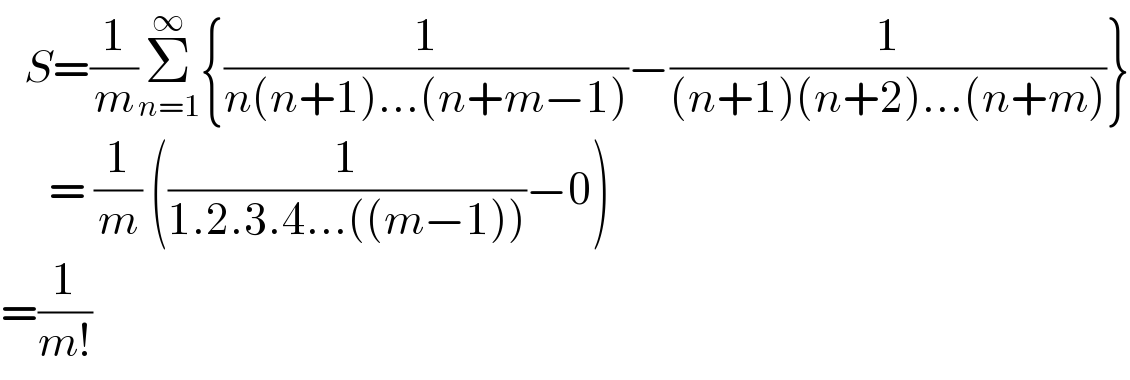
S=(1/m)Σ_(n=1) ^∞ {(1/(n(n+1)...(n+m−1)))−(1/((n+1)(n+2)...(n+m)))} = (1/m) ((1/(1.2.3.4...((m−1))))−0) =(1/(m!))

$$\:\:\:{S}=\frac{\mathrm{1}}{{m}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left\{\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)...\left({n}+{m}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)...\left({n}+{m}\right)}\right\} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{{m}}\:\left(\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}...\left(\left({m}−\mathrm{1}\right)\right)}−\mathrm{0}\right) \\ $$$$=\frac{\mathrm{1}}{{m}!} \\ $$

Commented by SANOGO last updated on 14/Dec/22

merci

$${merci} \\ $$

Commented by dre23 last updated on 15/Dec/22

n=1 we get (1/(mm!))

$${n}=\mathrm{1}\:{we}\:{get}\:\frac{\mathrm{1}}{{mm}!} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com