
Question Number 189263 by Gbenga last updated on 14/Mar/23
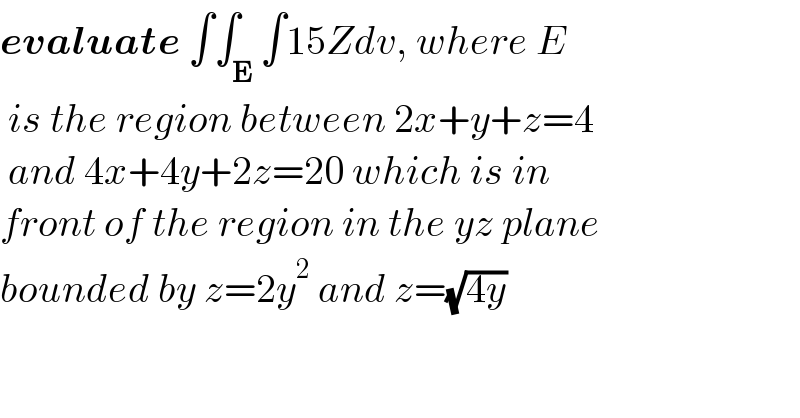
$$\boldsymbol{{evaluate}}\:\int\int_{\boldsymbol{\mathrm{E}}} \int\mathrm{15}{Zdv},\:{where}\:{E} \\ $$$$\:{is}\:{the}\:{region}\:{between}\:\mathrm{2}{x}+{y}+{z}=\mathrm{4} \\ $$$$\:{and}\:\mathrm{4}{x}+\mathrm{4}{y}+\mathrm{2}{z}=\mathrm{20}\:{which}\:{is}\:{in}\: \\ $$$${front}\:{of}\:{the}\:{region}\:{in}\:{the}\:{yz}\:{plane}\: \\ $$$${bounded}\:{by}\:{z}=\mathrm{2}{y}^{\mathrm{2}} \:{and}\:{z}=\sqrt{\mathrm{4}{y}} \\ $$
Commented by Gbenga last updated on 15/Mar/23
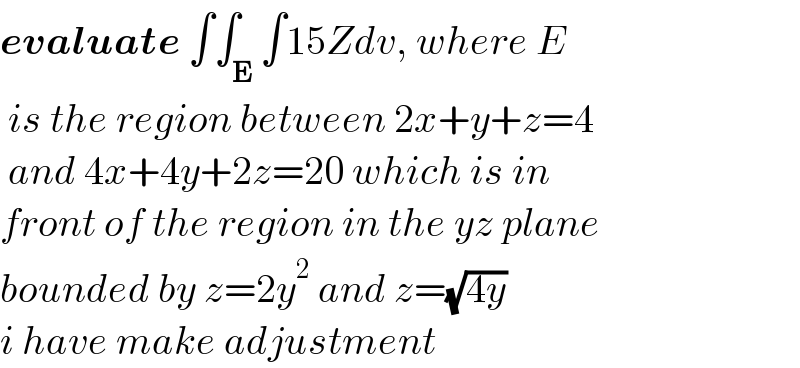
$$\boldsymbol{{evaluate}}\:\int\int_{\boldsymbol{\mathrm{E}}} \int\mathrm{15}{Zdv},\:{where}\:{E} \\ $$$$\:{is}\:{the}\:{region}\:{between}\:\mathrm{2}{x}+{y}+{z}=\mathrm{4} \\ $$$$\:{and}\:\mathrm{4}{x}+\mathrm{4}{y}+\mathrm{2}{z}=\mathrm{20}\:{which}\:{is}\:{in}\: \\ $$$${front}\:{of}\:{the}\:{region}\:{in}\:{the}\:{yz}\:{plane}\: \\ $$$${bounded}\:{by}\:{z}=\mathrm{2}{y}^{\mathrm{2}} \:{and}\:{z}=\sqrt{\mathrm{4}{y}} \\ $$$${i}\:{have}\:{make}\:{adjustment} \\ $$
