Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214051 by issac last updated on 25/Nov/24

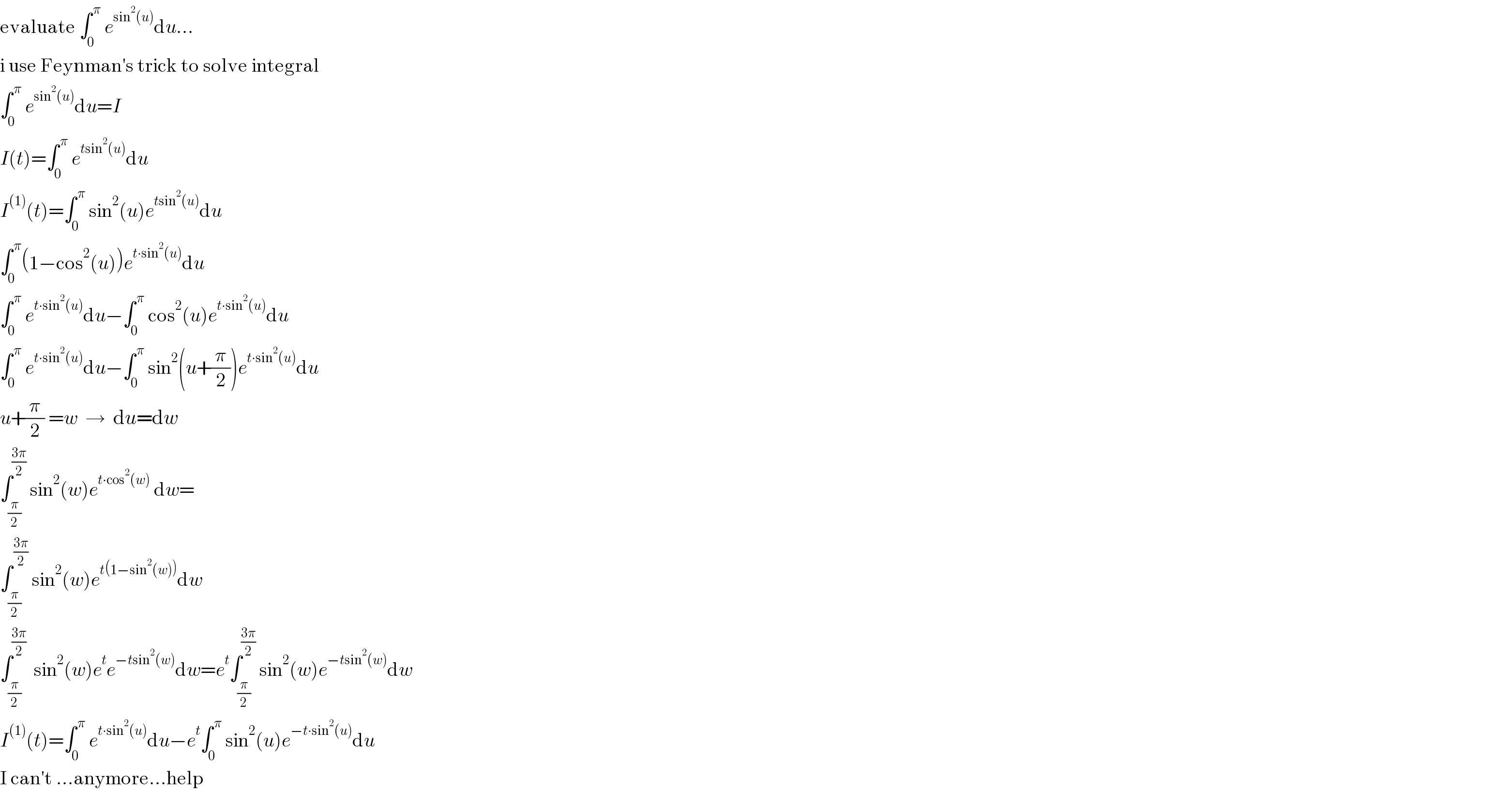
evaluate ∫_0 ^( π) e^(sin^2 (u)) du... i use Feynman′s trick to solve integral ∫_0 ^( π) e^(sin^2 (u)) du=I I(t)=∫_0 ^( π) e^(tsin^2 (u)) du I^((1)) (t)=∫_0 ^( π) sin^2 (u)e^(tsin^2 (u)) du ∫_0 ^( π) (1−cos^2 (u))e^(t∙sin^2 (u)) du ∫_0 ^( π) e^(t∙sin^2 (u)) du−∫_0 ^( π) cos^2 (u)e^(t∙sin^2 (u)) du ∫_0 ^( π) e^(t∙sin^2 (u)) du−∫_0 ^( π) sin^2 (u+(π/2))e^(t∙sin^2 (u)) du u+(π/2) =w → du=dw ∫_(π/2) ^((3π)/2) sin^2 (w)e^(t∙cos^2 (w)) dw= ∫_(π/2) ^( ((3π)/2)) sin^2 (w)e^(t(1−sin^2 (w))) dw ∫_(π/2) ^((3π)/2) sin^2 (w)e^t e^(−tsin^2 (w)) dw=e^t ∫_(π/2) ^((3π)/2) sin^2 (w)e^(−tsin^2 (w)) dw I^((1)) (t)=∫_0 ^( π) e^(t∙sin^2 (u)) du−e^t ∫_0 ^( π) sin^2 (u)e^(−t∙sin^2 (u)) du I can′t ...anymore...help

$$\mathrm{evaluate}\:\int_{\mathrm{0}} ^{\:\pi} \:{e}^{\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u}...\: \\ $$$$\mathrm{i}\:\mathrm{use}\:\mathrm{Feynman}'\mathrm{s}\:\mathrm{trick}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{integral} \\ $$$$\int_{\mathrm{0}} ^{\:\pi} \:{e}^{\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u}={I} \\ $$$${I}\left({t}\right)=\int_{\mathrm{0}} ^{\:\pi} \:{e}^{{t}\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u} \\ $$$${I}^{\left(\mathrm{1}\right)} \left({t}\right)=\int_{\mathrm{0}} ^{\:\pi} \:\mathrm{sin}^{\mathrm{2}} \left({u}\right){e}^{{t}\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u} \\ $$$$\int_{\mathrm{0}} ^{\:\pi} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left({u}\right)\right){e}^{{t}\centerdot\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u} \\ $$$$\int_{\mathrm{0}} ^{\:\pi} \:{e}^{{t}\centerdot\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u}−\int_{\mathrm{0}} ^{\:\pi} \:\mathrm{cos}^{\mathrm{2}} \left({u}\right){e}^{{t}\centerdot\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u} \\ $$$$\int_{\mathrm{0}} ^{\:\pi} \:{e}^{{t}\centerdot\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u}−\int_{\mathrm{0}} ^{\:\pi} \:\mathrm{sin}^{\mathrm{2}} \left({u}+\frac{\pi}{\mathrm{2}}\right){e}^{{t}\centerdot\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u} \\ $$$${u}+\frac{\pi}{\mathrm{2}}\:={w}\:\:\rightarrow\:\:\mathrm{d}{u}=\mathrm{d}{w} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2}} \left({w}\right){e}^{{t}\centerdot\mathrm{cos}^{\mathrm{2}} \left({w}\right)} \:\mathrm{d}{w}= \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\:\frac{\mathrm{3}\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2}} \left({w}\right){e}^{{t}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left({w}\right)\right)} \mathrm{d}{w} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \:\:\mathrm{sin}^{\mathrm{2}} \left({w}\right){e}^{{t}} {e}^{−{t}\mathrm{sin}^{\mathrm{2}} \left({w}\right)} \mathrm{d}{w}={e}^{{t}} \int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2}} \left({w}\right){e}^{−{t}\mathrm{sin}^{\mathrm{2}} \left({w}\right)} \mathrm{d}{w} \\ $$$${I}^{\left(\mathrm{1}\right)} \left({t}\right)=\int_{\mathrm{0}} ^{\:\pi} \:{e}^{{t}\centerdot\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u}−{e}^{{t}} \int_{\mathrm{0}} ^{\:\pi} \:\mathrm{sin}^{\mathrm{2}} \left({u}\right){e}^{−{t}\centerdot\mathrm{sin}^{\mathrm{2}} \left({u}\right)} \mathrm{d}{u} \\ $$$$\mathrm{I}\:\mathrm{can}'\mathrm{t}\:...\mathrm{anymore}...\mathrm{help} \\ $$

Commented by Ghisom last updated on 26/Nov/24

Feynman can′t help here

$$\mathrm{Feynman}\:\mathrm{can}'\mathrm{t}\:\mathrm{help}\:\mathrm{here} \\ $$

Answered by Ghisom last updated on 26/Nov/24

∫_0 ^π e^(sin^2 x) dx=2∫_0 ^(π/2) e^(sin^2 x) dx= [t=2x+π] =(√e)∫_π ^(2π) e^((1/2)cos t) dt=(√e)∫_0 ^π e^((1/2)cos t) dt Modified Bessel Function of the 1^(st) Kind I_n (z)=(1/π)∫_0 ^π e^(zcos θ) cos (nθ) dθ in our case n=0∧z=(1/2) ⇒ (√e)∫_0 ^π e^((1/2)cos t) dt=(√e)πI_0 ((1/2))

$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{e}^{\mathrm{sin}^{\mathrm{2}} \:{x}} {dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{e}^{\mathrm{sin}^{\mathrm{2}} \:{x}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}{x}+\pi\right] \\ $$$$=\sqrt{\mathrm{e}}\underset{\pi} {\overset{\mathrm{2}\pi} {\int}}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{t}} {dt}=\sqrt{\mathrm{e}}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{t}} {dt} \\ $$$$\mathrm{Modified}\:\mathrm{Bessel}\:\mathrm{Function}\:\mathrm{of}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{Kind} \\ $$$${I}_{{n}} \left({z}\right)=\frac{\mathrm{1}}{\pi}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{e}^{{z}\mathrm{cos}\:\theta} \mathrm{cos}\:\left({n}\theta\right)\:{d}\theta \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:{n}=\mathrm{0}\wedge{z}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\sqrt{\mathrm{e}}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{t}} {dt}=\sqrt{\mathrm{e}}\pi{I}_{\mathrm{0}} \:\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Commented by issac last updated on 27/Nov/24

wow thx

$${wow}\:{thx} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com