
Question Number 132091 by rs4089 last updated on 11/Feb/21
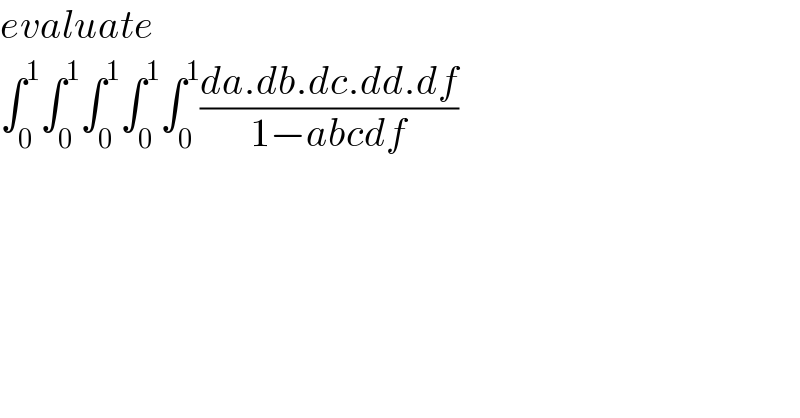
$${evaluate}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{da}.{db}.{dc}.{dd}.{df}}{\mathrm{1}−{abcdf}} \\ $$
Answered by Dwaipayan Shikari last updated on 11/Feb/21

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{5}} }=\zeta\left(\mathrm{5}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 11/Feb/21
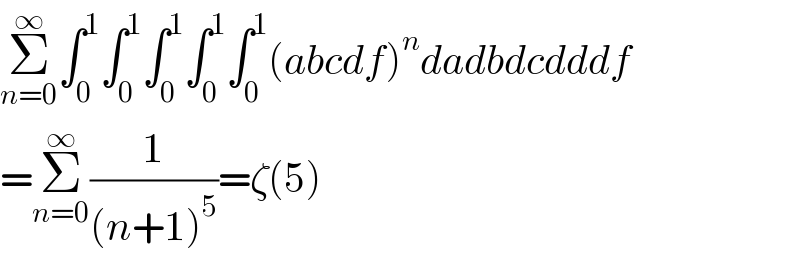
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left({abcdf}\right)^{{n}} {dadbdcdddf} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{5}} }=\zeta\left(\mathrm{5}\right) \\ $$
