
Question Number 124438 by Ar Brandon last updated on 03/Dec/20
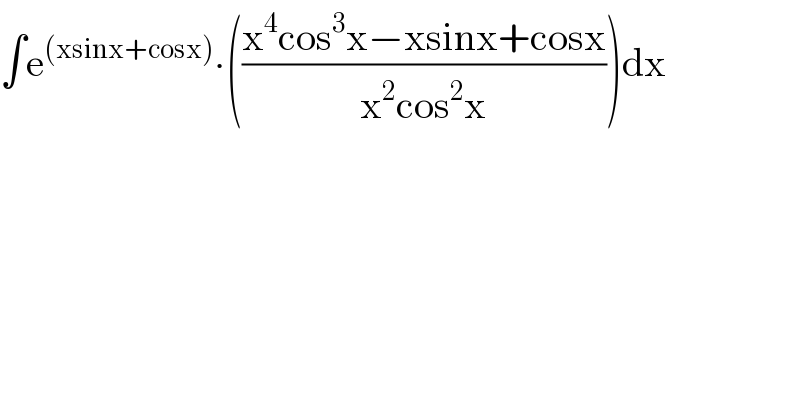
$$\int\mathrm{e}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} \centerdot\left(\frac{\mathrm{x}^{\mathrm{4}} \mathrm{cos}^{\mathrm{3}} \mathrm{x}−\mathrm{xsinx}+\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20

$${IIT}−{JEE}\:{book}? \\ $$
Commented by Ar Brandon last updated on 03/Dec/20
Yeah ��������
Answered by Ar Brandon last updated on 03/Dec/20
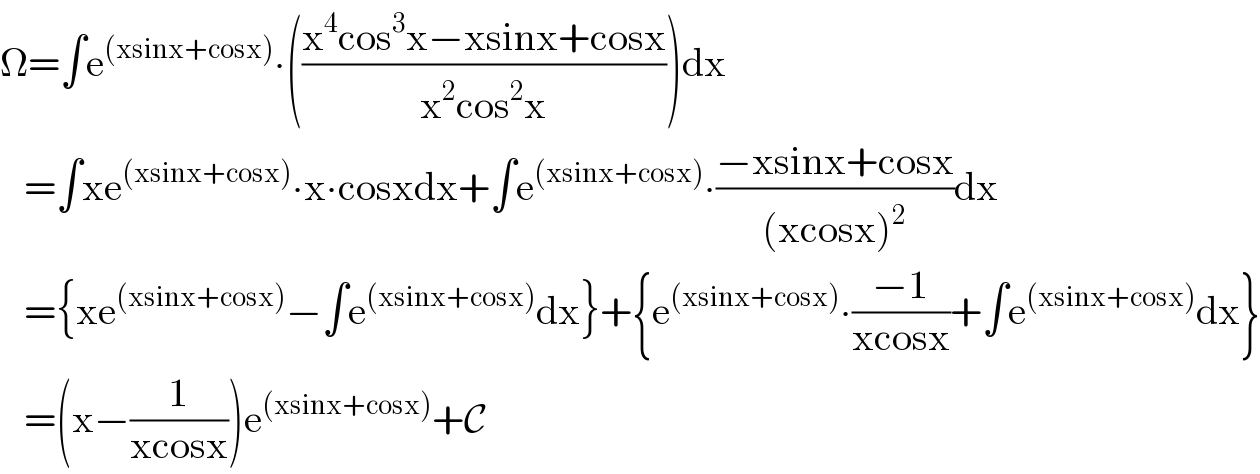
$$\Omega=\int\mathrm{e}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} \centerdot\left(\frac{\mathrm{x}^{\mathrm{4}} \mathrm{cos}^{\mathrm{3}} \mathrm{x}−\mathrm{xsinx}+\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx} \\ $$$$\:\:\:=\int\mathrm{xe}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} \centerdot\mathrm{x}\centerdot\mathrm{cosxdx}+\int\mathrm{e}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} \centerdot\frac{−\mathrm{xsinx}+\mathrm{cosx}}{\left(\mathrm{xcosx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:=\left\{\mathrm{xe}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} −\int\mathrm{e}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} \mathrm{dx}\right\}+\left\{\mathrm{e}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} \centerdot\frac{−\mathrm{1}}{\mathrm{xcosx}}+\int\mathrm{e}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} \mathrm{dx}\right\} \\ $$$$\:\:\:=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{xcosx}}\right)\mathrm{e}^{\left(\mathrm{xsinx}+\mathrm{cosx}\right)} +\mathcal{C} \\ $$
