
Question Number 195652 by mustafazaheen last updated on 06/Aug/23
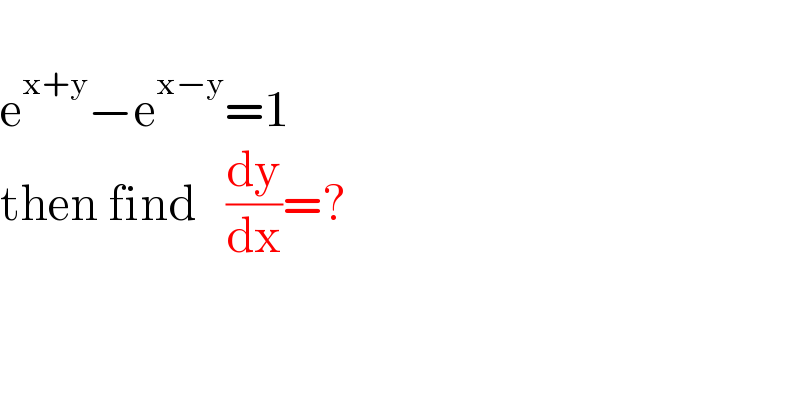
$$ \\ $$$$\mathrm{e}^{\mathrm{x}+\mathrm{y}} −\mathrm{e}^{\mathrm{x}−\mathrm{y}} =\mathrm{1} \\ $$$$\mathrm{then}\:\mathrm{find}\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=? \\ $$$$ \\ $$$$ \\ $$
Answered by MM42 last updated on 06/Aug/23
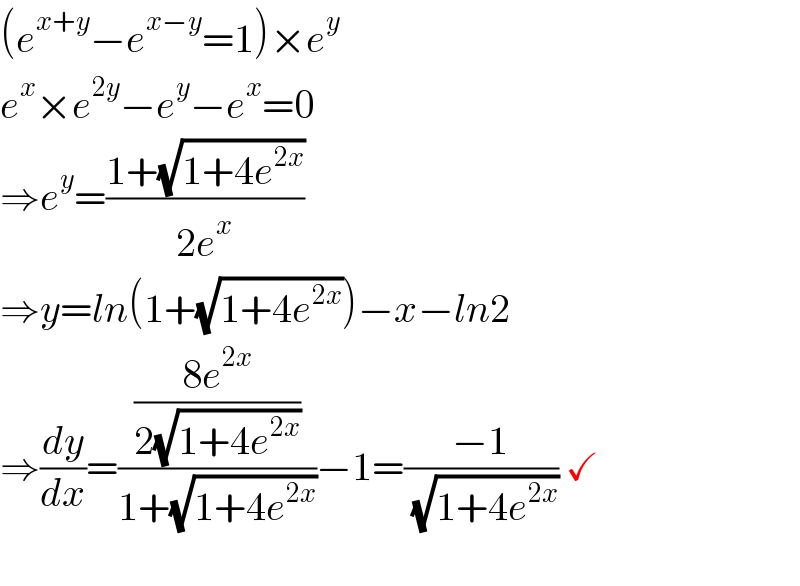
$$\left({e}^{{x}+{y}} −{e}^{{x}−{y}} =\mathrm{1}\right)×{e}^{{y}} \\ $$$${e}^{{x}} ×{e}^{\mathrm{2}{y}} −{e}^{{y}} −{e}^{{x}} =\mathrm{0} \\ $$$$\Rightarrow{e}^{{y}} =\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{e}^{\mathrm{2}{x}} }}{\mathrm{2}{e}^{{x}} } \\ $$$$\Rightarrow{y}={ln}\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{e}^{\mathrm{2}{x}} }\right)−{x}−{ln}\mathrm{2} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\frac{\mathrm{8}{e}^{\mathrm{2}{x}} }{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4}{e}^{\mathrm{2}{x}} }}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{e}^{\mathrm{2}{x}} }}−\mathrm{1}=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{e}^{\mathrm{2}{x}} }}\:\checkmark \\ $$$$ \\ $$
Answered by mahdipoor last updated on 06/Aug/23
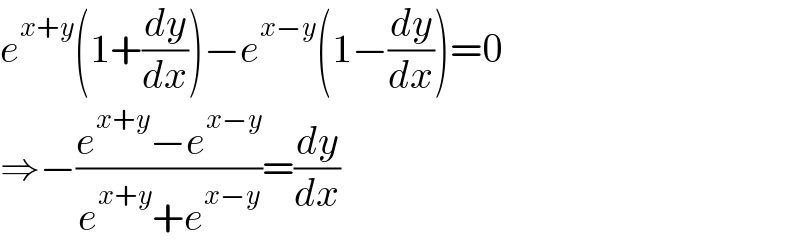
$${e}^{{x}+{y}} \left(\mathrm{1}+\frac{{dy}}{{dx}}\right)−{e}^{{x}−{y}} \left(\mathrm{1}−\frac{{dy}}{{dx}}\right)=\mathrm{0} \\ $$$$\Rightarrow−\frac{{e}^{{x}+{y}} −{e}^{{x}−{y}} }{{e}^{{x}+{y}} +{e}^{{x}−{y}} }=\frac{{dy}}{{dx}} \\ $$
