
Question Number 1000 by rpatle69@gmail.com last updated on 13/May/15
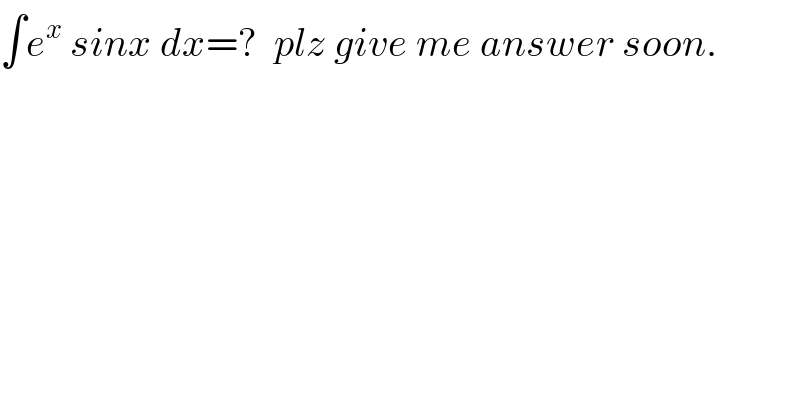
$$\int{e}^{{x}\:\:} {sinx}\:{dx}=?\:\:{plz}\:{give}\:{me}\:{answer}\:{soon}. \\ $$
Commented by rpatle69@gmail.com last updated on 13/May/15

$${please}\:{soon}\:{guys} \\ $$
Answered by prakash jain last updated on 13/May/15
![I=∫e^x sin xdx Integrate by parts I=e^x (−cos x)+∫e^x cos xdx Integrate e^x cos x by parts =−e^x cos x+e^x sin x−∫e^x sin xdx =−e^x cos x+e^x sin x−I 2I=e^x sin x−e^x cos x I=(1/2)(e^x sin x−e^x cos x)+C (d/dx)[(1/2)(e^x sin x−e^x cos x)+C] =(1/2)[e^x sin x+e^x cos x−e^x cos x+e^x sin x] =e^x sin x](Q1005.png)
$${I}=\int{e}^{{x}} \mathrm{sin}\:{xdx} \\ $$$${I}\mathrm{ntegrate}\:\mathrm{by}\:\mathrm{parts} \\ $$$${I}={e}^{{x}} \left(−\mathrm{cos}\:{x}\right)+\int{e}^{{x}} \mathrm{cos}\:{xdx} \\ $$$${I}\mathrm{ntegrate}\:{e}^{{x}} \mathrm{cos}\:{x}\:{by}\:{parts} \\ $$$$=−{e}^{{x}} \mathrm{cos}\:{x}+{e}^{{x}} \mathrm{sin}\:{x}−\int{e}^{{x}} \mathrm{sin}\:{xdx} \\ $$$$=−{e}^{{x}} \mathrm{cos}\:{x}+{e}^{{x}} \mathrm{sin}\:{x}−{I} \\ $$$$\mathrm{2}{I}={e}^{{x}} \mathrm{sin}\:{x}−{e}^{{x}} \mathrm{cos}\:{x} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{x}} \mathrm{sin}\:{x}−{e}^{{x}} \mathrm{cos}\:{x}\right)+{C} \\ $$$$\frac{{d}}{{dx}}\left[\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{x}} \mathrm{sin}\:{x}−{e}^{{x}} \mathrm{cos}\:{x}\right)+{C}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{e}^{{x}} \mathrm{sin}\:{x}+{e}^{{x}} \mathrm{cos}\:{x}−{e}^{{x}} \mathrm{cos}\:{x}+{e}^{{x}} \mathrm{sin}\:{x}\right] \\ $$$$={e}^{{x}} \mathrm{sin}\:{x} \\ $$
Commented by rpatle69@gmail.com last updated on 13/May/15

$${thanks} \\ $$
