
Question Number 115696 by Dwaipayan Shikari last updated on 27/Sep/20

$$\mathrm{e}^{\mathrm{x}} =\mathrm{logx} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Sep/20
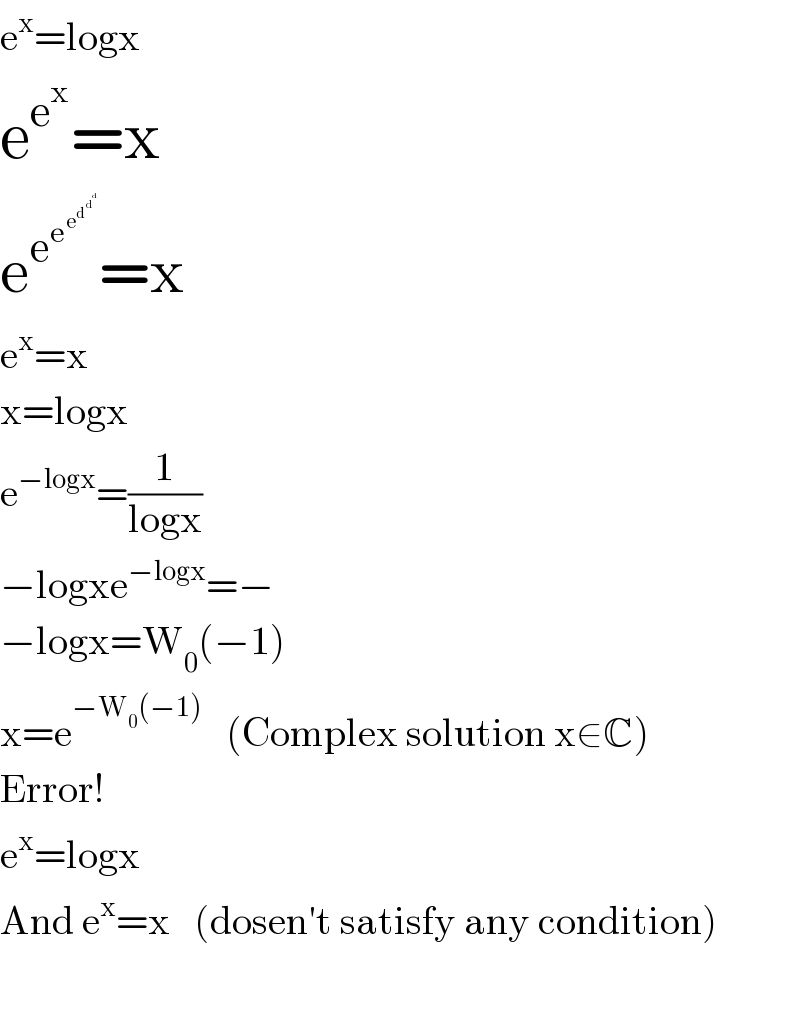
$$\mathrm{e}^{\mathrm{x}} =\mathrm{logx} \\ $$$$\mathrm{e}^{\mathrm{e}^{\mathrm{x}} } =\mathrm{x} \\ $$$$\mathrm{e}^{\mathrm{e}^{\mathrm{e}^{\mathrm{e}^{\mathrm{d}^{\mathrm{d}^{\mathrm{d}} } } } } } =\mathrm{x} \\ $$$$\mathrm{e}^{\mathrm{x}} =\mathrm{x} \\ $$$$\mathrm{x}=\mathrm{logx} \\ $$$$\mathrm{e}^{−\mathrm{logx}} =\frac{\mathrm{1}}{\mathrm{logx}} \\ $$$$−\mathrm{logxe}^{−\mathrm{logx}} =− \\ $$$$−\mathrm{logx}=\mathrm{W}_{\mathrm{0}} \left(−\mathrm{1}\right) \\ $$$$\mathrm{x}=\mathrm{e}^{−\mathrm{W}_{\mathrm{0}} \left(−\mathrm{1}\right)} \:\:\:\left(\mathrm{Complex}\:\mathrm{solution}\:\mathrm{x}\in\mathbb{C}\right) \\ $$$$\mathrm{Error}! \\ $$$$\mathrm{e}^{\mathrm{x}} =\mathrm{logx} \\ $$$$\mathrm{And}\:\mathrm{e}^{\mathrm{x}} =\mathrm{x}\:\:\:\left(\mathrm{dosen}'\mathrm{t}\:\mathrm{satisfy}\:\mathrm{any}\:\mathrm{condition}\right) \\ $$$$ \\ $$
Commented by TANMAY PANACEA last updated on 27/Sep/20
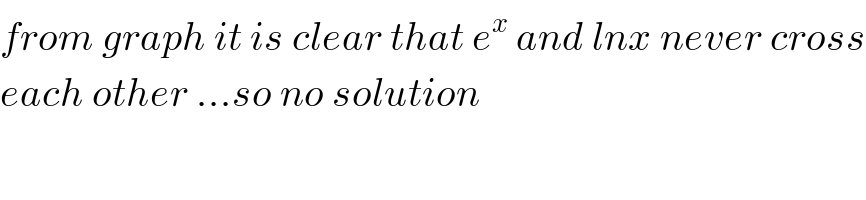
$${from}\:{graph}\:{it}\:{is}\:{clear}\:{that}\:{e}^{{x}} \:{and}\:{lnx}\:{never}\:{cross} \\ $$$${each}\:{other}\:...{so}\:{no}\:{solution} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Sep/20
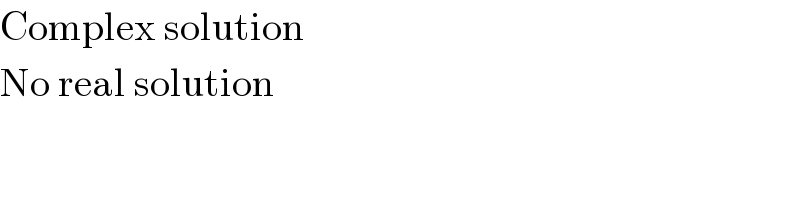
$$\mathrm{Complex}\:\mathrm{solution}\: \\ $$$$\mathrm{No}\:\mathrm{real}\:\mathrm{solution}\: \\ $$
Commented by TANMAY PANACEA last updated on 27/Sep/20

$${ok} \\ $$
