
Question Number 198001 by mathlove last updated on 07/Oct/23
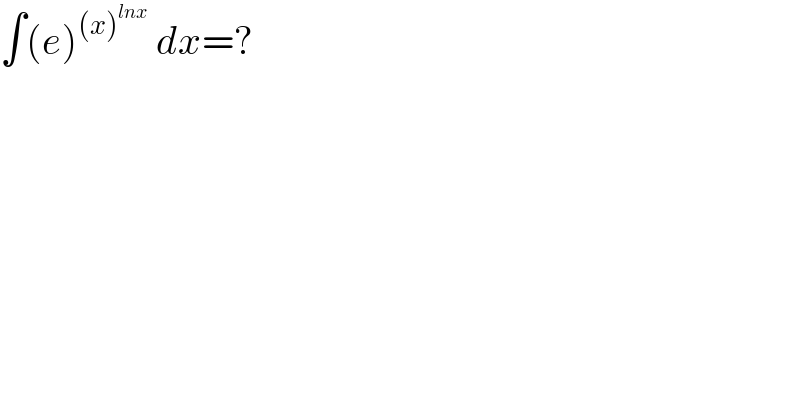
$$\int\left({e}\right)^{\left({x}\right)^{{lnx}} } \:{dx}=? \\ $$
Commented by Frix last updated on 07/Oct/23
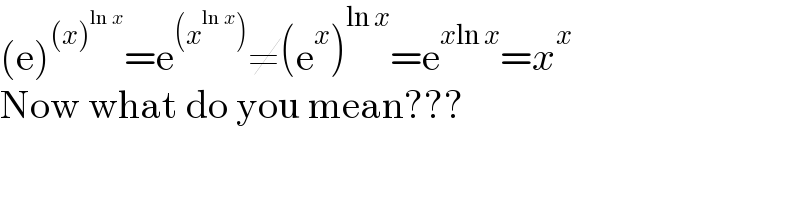
$$\left(\mathrm{e}\right)^{\left({x}\right)^{\mathrm{ln}\:{x}} } =\mathrm{e}^{\left({x}^{\mathrm{ln}\:{x}} \right)} \neq\left(\mathrm{e}^{{x}} \right)^{\mathrm{ln}\:{x}} =\mathrm{e}^{{x}\mathrm{ln}\:{x}} ={x}^{{x}} \\ $$$$\mathrm{Now}\:\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}??? \\ $$
Commented by mathlove last updated on 08/Oct/23

$${e}^{\left({x}^{{lnx}} \right)} \\ $$
