
Question Number 64579 by Tawa1 last updated on 19/Jul/19

$$\int\:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx} \\ $$$$ \\ $$$$\mathrm{can}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{close}\:\mathrm{form}\:\mathrm{of}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{or}\:\mathrm{analytic}\:\mathrm{solution} \\ $$
Commented by mathmax by abdo last updated on 19/Jul/19
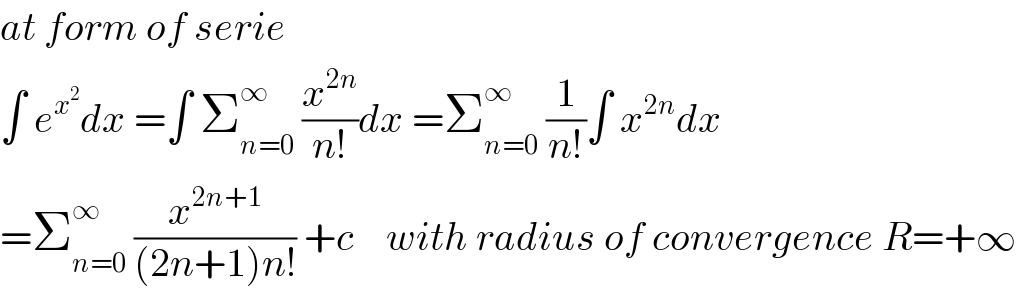
$${at}\:{form}\:{of}\:{serie} \\ $$$$\int\:{e}^{{x}^{\mathrm{2}} } {dx}\:=\int\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}} }{{n}!}{dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\int\:{x}^{\mathrm{2}{n}} {dx}\: \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\:+{c}\:\:\:\:{with}\:{radius}\:{of}\:{convergence}\:{R}=+\infty \\ $$
