
Question Number 143100 by lapache last updated on 10/Jun/21
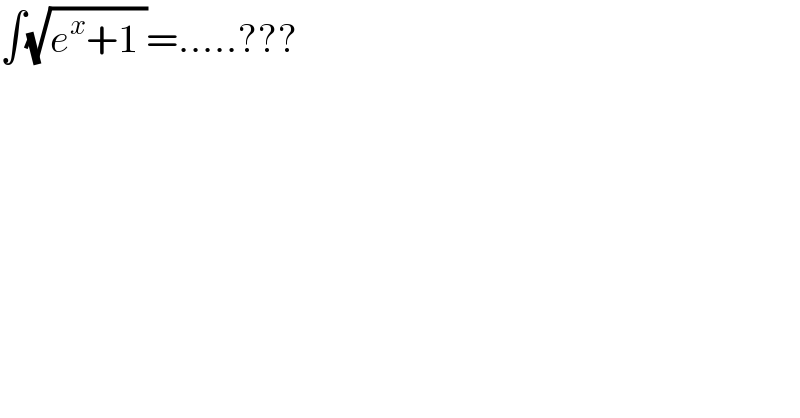
$$\int\sqrt{{e}^{{x}} +\mathrm{1}\:}=.....??? \\ $$
Answered by qaz last updated on 10/Jun/21
![∫(√(e^x +1))dx =∫(√(u+1))(du/u) =∫((u+1)/(u(√(u+1))))du =2(√(u+1))+∫(du/( u^2 (√((1/u)+(1/u^2 ))))) =2(√(u+1))−∫((d((1/u)))/( (√(((1/u)+(1/2))^2 −(1/4))))) =2(√(u+1))−∫((d[2((1/u)+(1/2))])/( (√([4((1/u)+(1/2))^2 −1])))) =2(√(u+1))−arccosh(2((1/u)+(1/2)))+C =2(√(e^x +1))−arccosh(((2+e^x )/e^x ))+C^](Q143121.png)
$$\int\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}\mathrm{dx} \\ $$$$=\int\sqrt{\mathrm{u}+\mathrm{1}}\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$=\int\frac{\mathrm{u}+\mathrm{1}}{\mathrm{u}\sqrt{\mathrm{u}+\mathrm{1}}}\mathrm{du} \\ $$$$=\mathrm{2}\sqrt{\mathrm{u}+\mathrm{1}}+\int\frac{\mathrm{du}}{\:\mathrm{u}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}}{\mathrm{u}}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{u}+\mathrm{1}}−\int\frac{\mathrm{d}\left(\frac{\mathrm{1}}{\mathrm{u}}\right)}{\:\sqrt{\left(\frac{\mathrm{1}}{\mathrm{u}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{u}+\mathrm{1}}−\int\frac{\mathrm{d}\left[\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{u}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right]}{\:\sqrt{\left[\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{u}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}\right]}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{u}+\mathrm{1}}−\mathrm{arccosh}\left(\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{u}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+\mathrm{C} \\ $$$$=\mathrm{2}\sqrt{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}−\mathrm{arccosh}\left(\frac{\mathrm{2}+\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} }\right)+\overset{} {\mathrm{C}} \\ $$
Answered by MJS_new last updated on 10/Jun/21
![∫(√(e^x +1))dx= [t=(√(e^x +1)) → dx=((2(√(e^x +1)))/e^x )dt] =2∫(t^2 /(t^2 −1))dt=∫(2+(1/(t−1))−(1/(t+1)))dt= =2t+ln ((t−1)/(t+1)) =... =2(√(e^x +1))−x+ln (e^x +2−2(√(e^x +1))) +C](Q143126.png)
$$\int\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}}{\mathrm{e}^{{x}} }{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}{dt}=\int\left(\mathrm{2}+\frac{\mathrm{1}}{{t}−\mathrm{1}}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}= \\ $$$$=\mathrm{2}{t}+\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\:=... \\ $$$$=\mathrm{2}\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}−{x}+\mathrm{ln}\:\left(\mathrm{e}^{{x}} +\mathrm{2}−\mathrm{2}\sqrt{\mathrm{e}^{{x}} +\mathrm{1}}\right)\:+{C} \\ $$
Answered by pticantor last updated on 10/Jun/21

$${wokooo}\:{et}\:{tu}\:{veux}\:{le}\:{riz}\:{pour}\:{casser}\:{sa}\:{hein} \\ $$$${tu}\:{vas}\:{lire}?{l}'{heure} \\ $$
Answered by mathmax by abdo last updated on 11/Jun/21
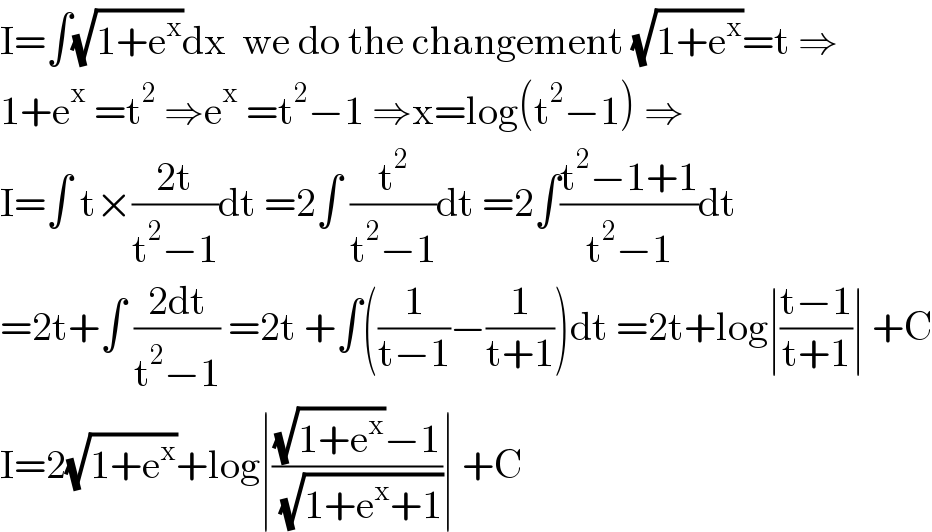
$$\mathrm{I}=\int\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{1}+\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\mathrm{x}=\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{I}=\int\:\mathrm{t}×\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:=\mathrm{2}\int\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:=\mathrm{2}\int\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt} \\ $$$$=\mathrm{2t}+\int\:\frac{\mathrm{2dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{2t}\:+\int\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt}\:=\mathrm{2t}+\mathrm{log}\mid\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mid\:+\mathrm{C} \\ $$$$\mathrm{I}=\mathrm{2}\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }+\mathrm{log}\mid\frac{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }−\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} +\mathrm{1}}}\mid\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 11/Jun/21
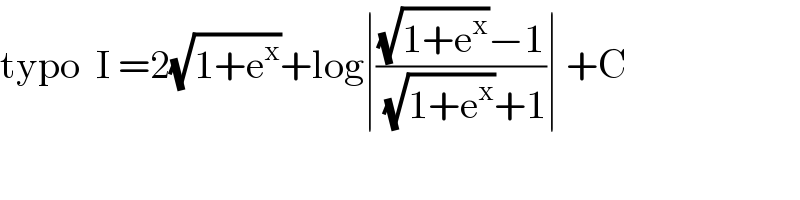
$$\mathrm{typo}\:\:\mathrm{I}\:=\mathrm{2}\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }+\mathrm{log}\mid\frac{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }−\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }+\mathrm{1}}\mid\:+\mathrm{C} \\ $$
Answered by puissant last updated on 23/Aug/21
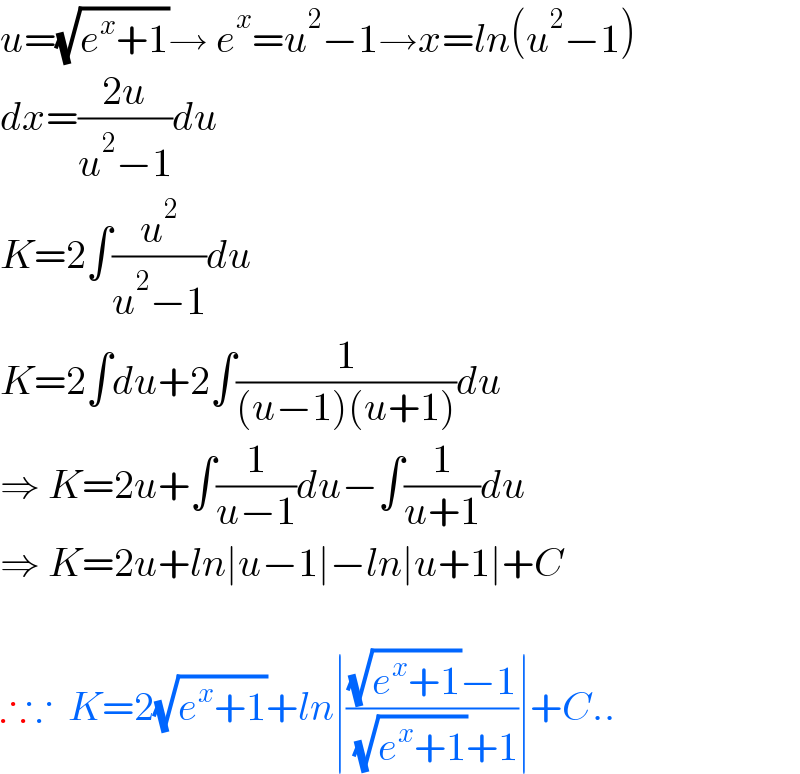
$${u}=\sqrt{{e}^{{x}} +\mathrm{1}}\rightarrow\:{e}^{{x}} ={u}^{\mathrm{2}} −\mathrm{1}\rightarrow{x}={ln}\left({u}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${dx}=\frac{\mathrm{2}{u}}{{u}^{\mathrm{2}} −\mathrm{1}}{du} \\ $$$${K}=\mathrm{2}\int\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} −\mathrm{1}}{du} \\ $$$${K}=\mathrm{2}\int{du}+\mathrm{2}\int\frac{\mathrm{1}}{\left({u}−\mathrm{1}\right)\left({u}+\mathrm{1}\right)}{du} \\ $$$$\Rightarrow\:{K}=\mathrm{2}{u}+\int\frac{\mathrm{1}}{{u}−\mathrm{1}}{du}−\int\frac{\mathrm{1}}{{u}+\mathrm{1}}{du} \\ $$$$\Rightarrow\:{K}=\mathrm{2}{u}+{ln}\mid{u}−\mathrm{1}\mid−{ln}\mid{u}+\mathrm{1}\mid+{C} \\ $$$$ \\ $$$$\therefore\because\:\:{K}=\mathrm{2}\sqrt{{e}^{{x}} +\mathrm{1}}+{ln}\mid\frac{\sqrt{{e}^{{x}} +\mathrm{1}}−\mathrm{1}}{\:\sqrt{{e}^{{x}} +\mathrm{1}}+\mathrm{1}}\mid+{C}.. \\ $$
