Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 215498 by alephnull last updated on 08/Jan/25

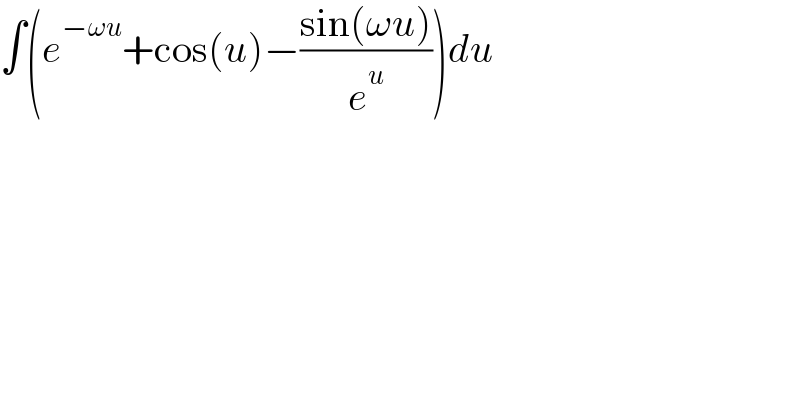
∫(e^(−ωu) +cos(u)−((sin(ωu))/e^u ))du

$$\int\left({e}^{−\omega{u}} +\mathrm{cos}\left({u}\right)−\frac{\mathrm{sin}\left(\omega{u}\right)}{{e}^{{u}} }\right){du} \\ $$

Answered by MathematicalUser2357 last updated on 10/Jan/25

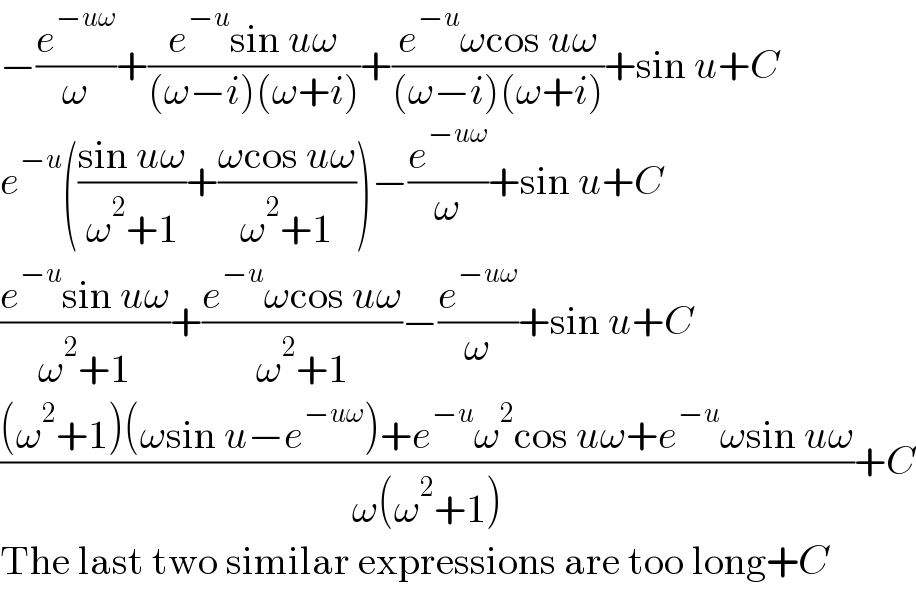
−(e^(−uω) /ω)+((e^(−u) sin uω)/((ω−i)(ω+i)))+((e^(−u) ωcos uω)/((ω−i)(ω+i)))+sin u+C e^(−u) (((sin uω)/(ω^2 +1))+((ωcos uω)/(ω^2 +1)))−(e^(−uω) /ω)+sin u+C ((e^(−u) sin uω)/(ω^2 +1))+((e^(−u) ωcos uω)/(ω^2 +1))−(e^(−uω) /ω)+sin u+C (((ω^2 +1)(ωsin u−e^(−uω) )+e^(−u) ω^2 cos uω+e^(−u) ωsin uω)/(ω(ω^2 +1)))+C The last two similar expressions are too long+C

$$−\frac{{e}^{−{u}\omega} }{\omega}+\frac{{e}^{−{u}} \mathrm{sin}\:{u}\omega}{\left(\omega−{i}\right)\left(\omega+{i}\right)}+\frac{{e}^{−{u}} \omega\mathrm{cos}\:{u}\omega}{\left(\omega−{i}\right)\left(\omega+{i}\right)}+\mathrm{sin}\:{u}+{C} \\ $$$${e}^{−{u}} \left(\frac{\mathrm{sin}\:{u}\omega}{\omega^{\mathrm{2}} +\mathrm{1}}+\frac{\omega\mathrm{cos}\:{u}\omega}{\omega^{\mathrm{2}} +\mathrm{1}}\right)−\frac{{e}^{−{u}\omega} }{\omega}+\mathrm{sin}\:{u}+{C} \\ $$$$\frac{{e}^{−{u}} \mathrm{sin}\:{u}\omega}{\omega^{\mathrm{2}} +\mathrm{1}}+\frac{{e}^{−{u}} \omega\mathrm{cos}\:{u}\omega}{\omega^{\mathrm{2}} +\mathrm{1}}−\frac{{e}^{−{u}\omega} }{\omega}+\mathrm{sin}\:{u}+{C} \\ $$$$\frac{\left(\omega^{\mathrm{2}} +\mathrm{1}\right)\left(\omega\mathrm{sin}\:{u}−{e}^{−{u}\omega} \right)+{e}^{−{u}} \omega^{\mathrm{2}} \mathrm{cos}\:{u}\omega+{e}^{−{u}} \omega\mathrm{sin}\:{u}\omega}{\omega\left(\omega^{\mathrm{2}} +\mathrm{1}\right)}+{C} \\ $$$$\mathrm{The}\:\mathrm{last}\:\mathrm{two}\:\mathrm{similar}\:\mathrm{expressions}\:\mathrm{are}\:\mathrm{too}\:\mathrm{long}+{C} \\ $$

Answered by mr W last updated on 10/Jan/25

I=∫((sin (ωu))/e^u )du I=−(1/ω)∫(1/e^u )d(cos (ωu)) I=−(1/ω)[((cos (ωu))/e^u )+∫((cos (ωu)du)/e^u )] I=−(1/ω)[((cos (ωu))/e^u )+(1/ω)∫((d(sin (ωu))/e^u )] I=−(1/ω)[((cos (ωu))/e^u )+(1/ω)×((sin (ωu))/e^u )+(1/ω)∫((sin (ωu))/e^u )du] I=−(1/ω^2 )[((sin (ωu)+ω cos (ωu))/e^u )+I] (ω^2 +1)I=−((sin (ωu)+ω cos (ωu))/e^u ) ⇒I=∫((sin (ωu))/e^u )du=−((sin (ωu)+ω cos (ωu))/((ω^2 +1)e^u )) ∫(e^(−ωu) +cos (u)−((sin (ωu))/e^u ))du =∫e^(−ωu) du+∫cos (u)du−∫((sin (ωu))/e^u )du =−(e^(−ωu) /ω)+sin u−∫((sin (ωu))/e^u )du =−(e^(−ωu) /ω)+sin u+((sin (ωu)+ω cos (ωu))/((ω^2 +1)e^u ))+C

$${I}=\int\frac{\mathrm{sin}\:\left(\omega{u}\right)}{{e}^{{u}} }{du} \\ $$$${I}=−\frac{\mathrm{1}}{\omega}\int\frac{\mathrm{1}}{{e}^{{u}} }{d}\left(\mathrm{cos}\:\left(\omega{u}\right)\right) \\ $$$${I}=−\frac{\mathrm{1}}{\omega}\left[\frac{\mathrm{cos}\:\left(\omega{u}\right)}{{e}^{{u}} }+\int\frac{\mathrm{cos}\:\left(\omega{u}\right){du}}{{e}^{{u}} }\right] \\ $$$${I}=−\frac{\mathrm{1}}{\omega}\left[\frac{\mathrm{cos}\:\left(\omega{u}\right)}{{e}^{{u}} }+\frac{\mathrm{1}}{\omega}\int\frac{{d}\left(\mathrm{sin}\:\left(\omega{u}\right)\right.}{{e}^{{u}} }\right] \\ $$$${I}=−\frac{\mathrm{1}}{\omega}\left[\frac{\mathrm{cos}\:\left(\omega{u}\right)}{{e}^{{u}} }+\frac{\mathrm{1}}{\omega}×\frac{\mathrm{sin}\:\left(\omega{u}\right)}{{e}^{{u}} }+\frac{\mathrm{1}}{\omega}\int\frac{\mathrm{sin}\:\left(\omega{u}\right)}{{e}^{{u}} }{du}\right] \\ $$$${I}=−\frac{\mathrm{1}}{\omega^{\mathrm{2}} }\left[\frac{\mathrm{sin}\:\left(\omega{u}\right)+\omega\:\mathrm{cos}\:\left(\omega{u}\right)}{{e}^{{u}} }+{I}\right] \\ $$$$\left(\omega^{\mathrm{2}} +\mathrm{1}\right){I}=−\frac{\mathrm{sin}\:\left(\omega{u}\right)+\omega\:\mathrm{cos}\:\left(\omega{u}\right)}{{e}^{{u}} } \\ $$$$\Rightarrow{I}=\int\frac{\mathrm{sin}\:\left(\omega{u}\right)}{{e}^{{u}} }{du}=−\frac{\mathrm{sin}\:\left(\omega{u}\right)+\omega\:\mathrm{cos}\:\left(\omega{u}\right)}{\left(\omega^{\mathrm{2}} +\mathrm{1}\right){e}^{{u}} } \\ $$$$ \\ $$$$\int\left({e}^{−\omega{u}} +\mathrm{cos}\:\left({u}\right)−\frac{\mathrm{sin}\:\left(\omega{u}\right)}{{e}^{{u}} }\right){du} \\ $$$$=\int{e}^{−\omega{u}} {du}+\int\mathrm{cos}\:\left({u}\right){du}−\int\frac{\mathrm{sin}\:\left(\omega{u}\right)}{{e}^{{u}} }{du} \\ $$$$=−\frac{{e}^{−\omega{u}} }{\omega}+\mathrm{sin}\:{u}−\int\frac{\mathrm{sin}\:\left(\omega{u}\right)}{{e}^{{u}} }{du} \\ $$$$=−\frac{{e}^{−\omega{u}} }{\omega}+\mathrm{sin}\:{u}+\frac{\mathrm{sin}\:\left(\omega{u}\right)+\omega\:\mathrm{cos}\:\left(\omega{u}\right)}{\left(\omega^{\mathrm{2}} +\mathrm{1}\right){e}^{{u}} }+{C} \\ $$

Commented by alephnull last updated on 10/Jan/25

thank

$${thank} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com