Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 129241 by BHOOPENDRA last updated on 14/Jan/21

(e^(−πs) /(s^2 (s^2 +1))) find inverse laplace

$$\frac{{e}^{−\pi{s}} }{{s}^{\mathrm{2}} \left({s}^{\mathrm{2}} +\mathrm{1}\right)}\:{find}\:{inverse}\:{laplace} \\ $$

Answered by Olaf last updated on 14/Jan/21

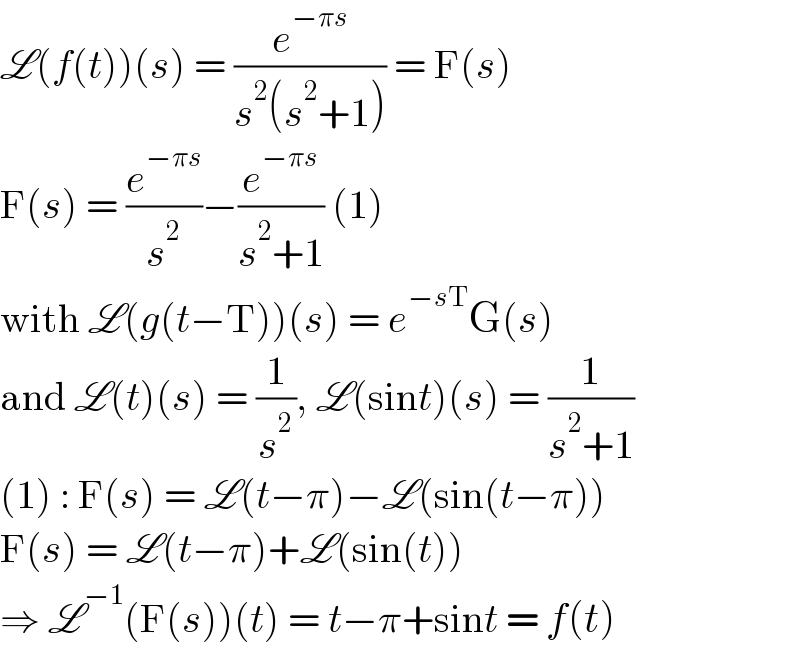
L(f(t))(s) = (e^(−πs) /(s^2 (s^2 +1))) = F(s) F(s) = (e^(−πs) /s^2 )−(e^(−πs) /(s^2 +1)) (1) with L(g(t−T))(s) = e^(−sT) G(s) and L(t)(s) = (1/s^2 ), L(sint)(s) = (1/(s^2 +1)) (1) : F(s) = L(t−π)−L(sin(t−π)) F(s) = L(t−π)+L(sin(t)) ⇒ L^(−1) (F(s))(t) = t−π+sint = f(t)

$$\mathscr{L}\left({f}\left({t}\right)\right)\left({s}\right)\:=\:\frac{{e}^{−\pi{s}} }{{s}^{\mathrm{2}} \left({s}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\mathrm{F}\left({s}\right) \\ $$$$\mathrm{F}\left({s}\right)\:=\:\frac{{e}^{−\pi{s}} }{{s}^{\mathrm{2}} }−\frac{{e}^{−\pi{s}} }{{s}^{\mathrm{2}} +\mathrm{1}}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{with}\:\mathscr{L}\left({g}\left({t}−\mathrm{T}\right)\right)\left({s}\right)\:=\:{e}^{−{s}\mathrm{T}} \mathrm{G}\left({s}\right) \\ $$$$\mathrm{and}\:\mathscr{L}\left({t}\right)\left({s}\right)\:=\:\frac{\mathrm{1}}{{s}^{\mathrm{2}} },\:\mathscr{L}\left(\mathrm{sin}{t}\right)\left({s}\right)\:=\:\frac{\mathrm{1}}{{s}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{F}\left({s}\right)\:=\:\mathscr{L}\left({t}−\pi\right)−\mathscr{L}\left(\mathrm{sin}\left({t}−\pi\right)\right) \\ $$$$\mathrm{F}\left({s}\right)\:=\:\mathscr{L}\left({t}−\pi\right)+\mathscr{L}\left(\mathrm{sin}\left({t}\right)\right) \\ $$$$\Rightarrow\:\mathscr{L}^{−\mathrm{1}} \left(\mathrm{F}\left({s}\right)\right)\left({t}\right)\:=\:{t}−\pi+\mathrm{sin}{t}\:=\:{f}\left({t}\right) \\ $$

Commented by BHOOPENDRA last updated on 14/Jan/21

Ans is not crct can you please recheck Ans is [(t−π)+sin(t−π)]×4(t−π)

$${Ans}\:{is}\:{not}\:{crct}\:{can}\:{you}\:{please}\:{recheck} \\ $$$${Ans}\:{is}\:\left[\left({t}−\pi\right)+{sin}\left({t}−\pi\right)\right]×\mathrm{4}\left({t}−\pi\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com