
Question Number 128885 by naka3546 last updated on 11/Jan/21

$${e}^{{e}^{{x}} } \:=\:{x} \\ $$$${x}\:=\:? \\ $$
Commented by naka3546 last updated on 11/Jan/21
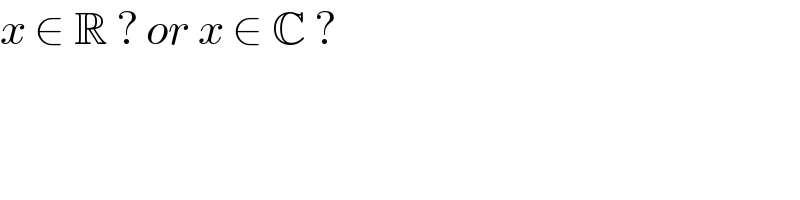
$${x}\:\in\:\mathbb{R}\:?\:{or}\:{x}\:\in\:\mathbb{C}\:? \\ $$
Commented by mr W last updated on 11/Jan/21
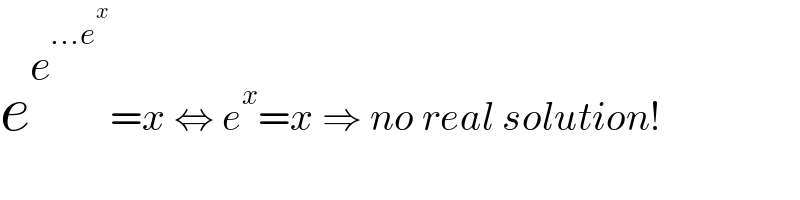
$${e}^{{e}^{...{e}^{{x}} } } ={x}\:\Leftrightarrow\:{e}^{{x}} ={x}\:\Rightarrow\:{no}\:{real}\:{solution}! \\ $$
Answered by mr W last updated on 11/Jan/21

$${e}^{{x}} ={x}\:\in\:\mathbb{C} \\ $$$$\Rightarrow{x}=\mathrm{ln}\:{x} \\ $$$${x}={re}^{{i}\theta} =\mathrm{ln}\:{r}+{i}\theta={r}\mathrm{cos}\:\theta+{r}\mathrm{sin}\:\theta\:{i} \\ $$$$\mathrm{ln}\:{r}={r}\:\mathrm{cos}\:\theta\:\Rightarrow{r}={e}^{{r}\:\mathrm{cos}\:\theta} \\ $$$$\theta={r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{r}=\frac{\theta}{\mathrm{sin}\:\theta}\:\:\:...\left({I}\right) \\ $$$$\Rightarrow\frac{\theta}{\mathrm{sin}\:\theta}={e}^{\frac{\theta}{\mathrm{tan}\:\theta}} \:\:\:...\left({II}\right) \\ $$$$\left(\theta,\:{r}\right)=\left(\pm\mathrm{1}.\mathrm{3372},\:\mathrm{1}.\mathrm{3746}\right),\:\left(\pm\mathrm{7}.\mathrm{5886},\:\mathrm{7}.\mathrm{8639}\right),\:... \\ $$$${there}\:{are}\:{infinite}\:{solutions}. \\ $$
