Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 62122 by aliesam last updated on 15/Jun/19

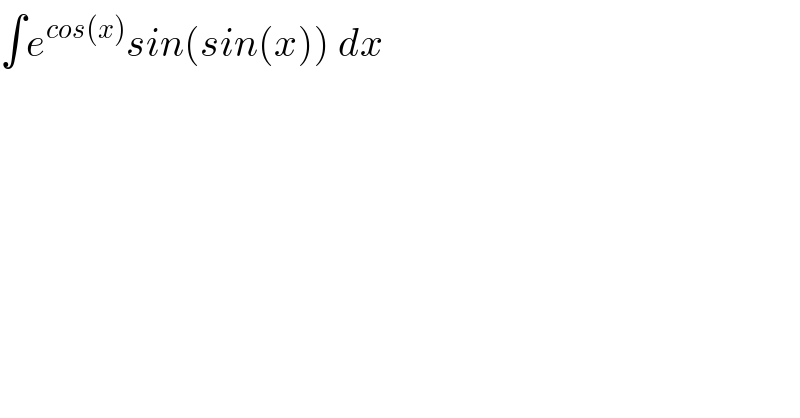
∫e^(cos(x)) sin(sin(x)) dx

$$\int{e}^{{cos}\left({x}\right)} {sin}\left({sin}\left({x}\right)\right)\:{dx}\: \\ $$

Commented by MJS last updated on 15/Jun/19

∫e^(cos x) sin sin x dx=−(i/2)∫(e^((e^(ix) −e^(−ix) )/2) −e^(−((e^(ix) −e^(−ix) )/2)) )e^((e^(ix) +e^(−ix) )/2) dx= =−(i/2)∫(e^e^(ix) −e^e^(−ix) )dx=−(i/2)∫e^e^(ix) dx+(i/2)∫e^e^(−ix) dx −(i/2)∫e^e^(ix) dx= [t=e^(ix) → dx=−ie^(−ix) dt] =−(1/2)∫(e^t /t)dt (i/2)∫e^e^(−ix) dx= [t=e^(−ix) → dx=ie^(ix) dt] =−(1/2)∫(e^t /t)dt ⇒ both lead to the incomplete gamma function

$$\int\mathrm{e}^{\mathrm{cos}\:{x}} \mathrm{sin}\:\mathrm{sin}\:{x}\:{dx}=−\frac{\mathrm{i}}{\mathrm{2}}\int\left(\mathrm{e}^{\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2}}} −\mathrm{e}^{−\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2}}} \right)\mathrm{e}^{\frac{\mathrm{e}^{\mathrm{i}{x}} +\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2}}} {dx}= \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\int\left(\mathrm{e}^{\mathrm{e}^{\mathrm{i}{x}} } −\mathrm{e}^{\mathrm{e}^{−\mathrm{i}{x}} } \right){dx}=−\frac{\mathrm{i}}{\mathrm{2}}\int\mathrm{e}^{\mathrm{e}^{\mathrm{i}{x}} } {dx}+\frac{\mathrm{i}}{\mathrm{2}}\int\mathrm{e}^{\mathrm{e}^{−\mathrm{i}{x}} } {dx} \\ $$$$ \\ $$$$−\frac{\mathrm{i}}{\mathrm{2}}\int\mathrm{e}^{\mathrm{e}^{\mathrm{i}{x}} } {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{\mathrm{i}{x}} \:\rightarrow\:{dx}=−\mathrm{ie}^{−\mathrm{i}{x}} {dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{e}^{{t}} }{{t}}{dt} \\ $$$$ \\ $$$$\frac{\mathrm{i}}{\mathrm{2}}\int\mathrm{e}^{\mathrm{e}^{−\mathrm{i}{x}} } {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{−\mathrm{i}{x}} \:\rightarrow\:{dx}=\mathrm{ie}^{\mathrm{i}{x}} {dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{e}^{{t}} }{{t}}{dt} \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{both}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{the}\:\mathrm{incomplete}\:\mathrm{gamma}\:\mathrm{function} \\ $$

Commented by aliesam last updated on 15/Jun/19

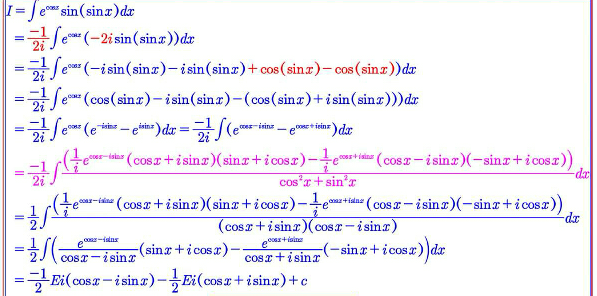
Commented by maxmathsup by imad last updated on 15/Jun/19

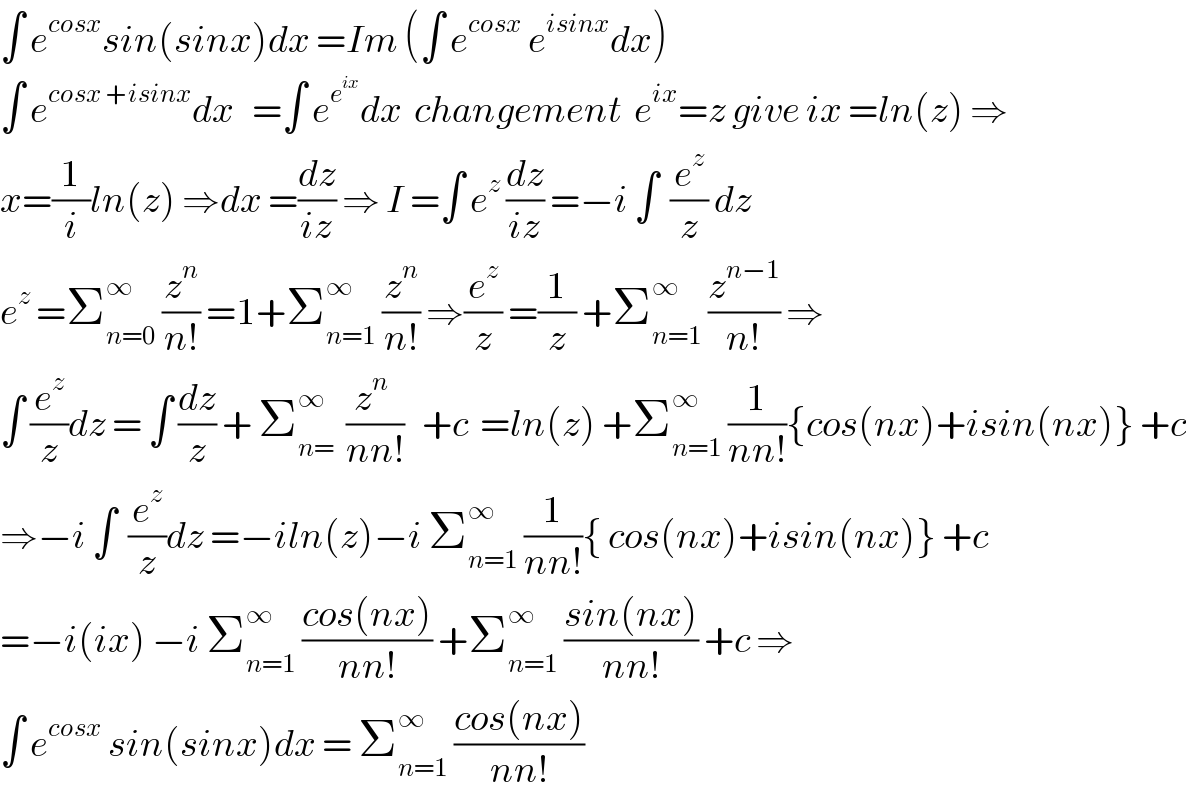
∫ e^(cosx) sin(sinx)dx =Im (∫ e^(cosx) e^(isinx) dx) ∫ e^(cosx +isinx) dx =∫ e^e^(ix) dx changement e^(ix) =z give ix =ln(z) ⇒ x=(1/i)ln(z) ⇒dx =(dz/(iz)) ⇒ I =∫ e^z (dz/(iz)) =−i ∫ (e^z /z) dz e^z =Σ_(n=0) ^∞ (z^n /(n!)) =1+Σ_(n=1) ^∞ (z^n /(n!)) ⇒(e^z /z) =(1/z) +Σ_(n=1) ^∞ (z^(n−1) /(n!)) ⇒ ∫ (e^z /z)dz = ∫ (dz/z) + Σ_(n=) ^∞ ((z^n )/(nn!)) +c =ln(z) +Σ_(n=1) ^∞ (1/(nn!)){cos(nx)+isin(nx)} +c ⇒−i ∫ (e^z /z)dz =−iln(z)−i Σ_(n=1) ^∞ (1/(nn!)){ cos(nx)+isin(nx)} +c =−i(ix) −i Σ_(n=1) ^∞ ((cos(nx))/(nn!)) +Σ_(n=1) ^∞ ((sin(nx))/(nn!)) +c ⇒ ∫ e^(cosx) sin(sinx)dx = Σ_(n=1) ^∞ ((cos(nx))/(nn!))

$$\int\:{e}^{{cosx}} {sin}\left({sinx}\right){dx}\:={Im}\:\left(\int\:{e}^{{cosx}} \:{e}^{{isinx}} {dx}\right) \\ $$$$\int\:{e}^{{cosx}\:+{isinx}} {dx}\:\:\:=\int\:{e}^{{e}^{{ix}} } {dx}\:\:{changement}\:\:{e}^{{ix}} ={z}\:{give}\:{ix}\:={ln}\left({z}\right)\:\Rightarrow \\ $$$${x}=\frac{\mathrm{1}}{{i}}{ln}\left({z}\right)\:\Rightarrow{dx}\:=\frac{{dz}}{{iz}}\:\Rightarrow\:{I}\:=\int\:{e}^{{z}} \:\frac{{dz}}{{iz}}\:=−{i}\:\int\:\:\frac{{e}^{{z}} }{{z}}\:{dz}\:\: \\ $$$${e}^{{z}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{z}^{{n}} }{{n}!}\:=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}} }{{n}!}\:\Rightarrow\frac{{e}^{{z}} }{{z}}\:=\frac{\mathrm{1}}{{z}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{n}−\mathrm{1}} }{{n}!}\:\Rightarrow \\ $$$$\int\:\frac{{e}^{{z}} }{{z}}{dz}\:=\:\int\:\frac{{dz}}{{z}}\:+\:\sum_{{n}=} ^{\infty} \:\:\frac{{z}^{{n}} \:}{{nn}!}\:\:\:+{c}\:\:={ln}\left({z}\right)\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{nn}!}\left\{{cos}\left({nx}\right)+{isin}\left({nx}\right)\right\}\:+{c} \\ $$$$\Rightarrow−{i}\:\int\:\:\frac{{e}^{{z}} }{{z}}{dz}\:=−{iln}\left({z}\right)−{i}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{nn}!}\left\{\:{cos}\left({nx}\right)+{isin}\left({nx}\right)\right\}\:+{c} \\ $$$$=−{i}\left({ix}\right)\:−{i}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{nn}!}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{nn}!}\:+{c}\:\Rightarrow \\ $$$$\int\:{e}^{{cosx}} \:{sin}\left({sinx}\right){dx}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{nn}!} \\ $$

Commented by maxmathsup by imad last updated on 16/Jun/19

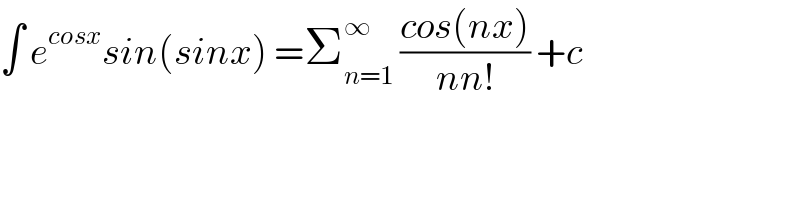
∫ e^(cosx) sin(sinx) =Σ_(n=1) ^∞ ((cos(nx))/(nn!)) +c

$$\int\:{e}^{{cosx}} {sin}\left({sinx}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{nn}!}\:+{c}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com