Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 126230 by I want to learn more last updated on 18/Dec/20

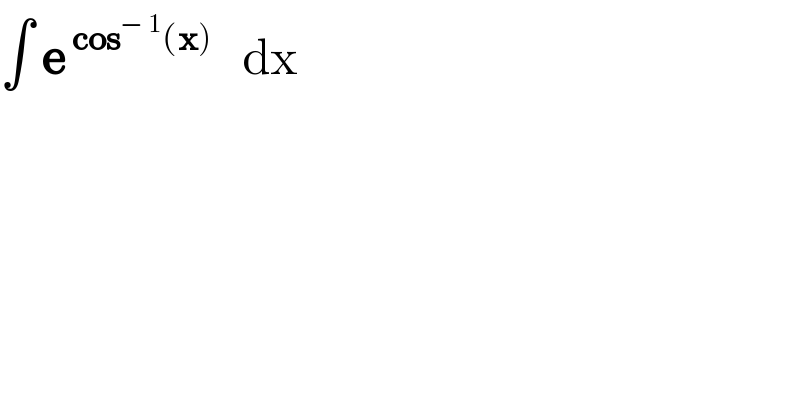
∫ e^( cos^(− 1) (x)) dx

$$\int\:\boldsymbol{\mathrm{e}}^{\:\boldsymbol{\mathrm{cos}}^{−\:\mathrm{1}} \left(\boldsymbol{\mathrm{x}}\right)} \:\:\:\mathrm{dx} \\ $$

Answered by Olaf last updated on 18/Dec/20

F(x) = ∫e^(arccosx) dx Let x = cosu, dx = −sinudu F(x) = −∫e^u sinudu F(x) = −[e^u sinu−∫e^u cosudu] F(x) = −e^u sinu+[e^u cosu−∫e^u (−sinudu] 2F(x) = e^u cosu−e^u sinu F(x) = (1/2)e^u (cosu−sinu) F(x) = (1/2)e^(arccosx) (x−sin(arccosx)) F(x) = (1/2)e^(arccosx) (x−(√(1−x^2 ))) (+C)

$$\mathrm{F}\left({x}\right)\:=\:\int{e}^{\mathrm{arccos}{x}} {dx} \\ $$$$\mathrm{Let}\:{x}\:=\:\mathrm{cos}{u},\:{dx}\:=\:−\mathrm{sin}{udu} \\ $$$$\mathrm{F}\left({x}\right)\:=\:−\int{e}^{{u}} \mathrm{sin}{udu} \\ $$$$\mathrm{F}\left({x}\right)\:=\:−\left[{e}^{{u}} \mathrm{sin}{u}−\int{e}^{{u}} \mathrm{cos}{udu}\right] \\ $$$$\mathrm{F}\left({x}\right)\:=\:−{e}^{{u}} \mathrm{sin}{u}+\left[{e}^{{u}} \mathrm{cos}{u}−\int{e}^{{u}} \left(−\mathrm{sin}{udu}\right]\right. \\ $$$$\mathrm{2F}\left({x}\right)\:=\:{e}^{{u}} \mathrm{cos}{u}−{e}^{{u}} \mathrm{sin}{u} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{{u}} \left(\mathrm{cos}{u}−\mathrm{sin}{u}\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{arccos}{x}} \left({x}−\mathrm{sin}\left(\mathrm{arccos}{x}\right)\right) \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{arccos}{x}} \left({x}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:\left(+\mathrm{C}\right) \\ $$

Commented by I want to learn more last updated on 18/Dec/20

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by I want to learn more last updated on 20/Dec/20

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Answered by mathmax by abdo last updated on 19/Dec/20

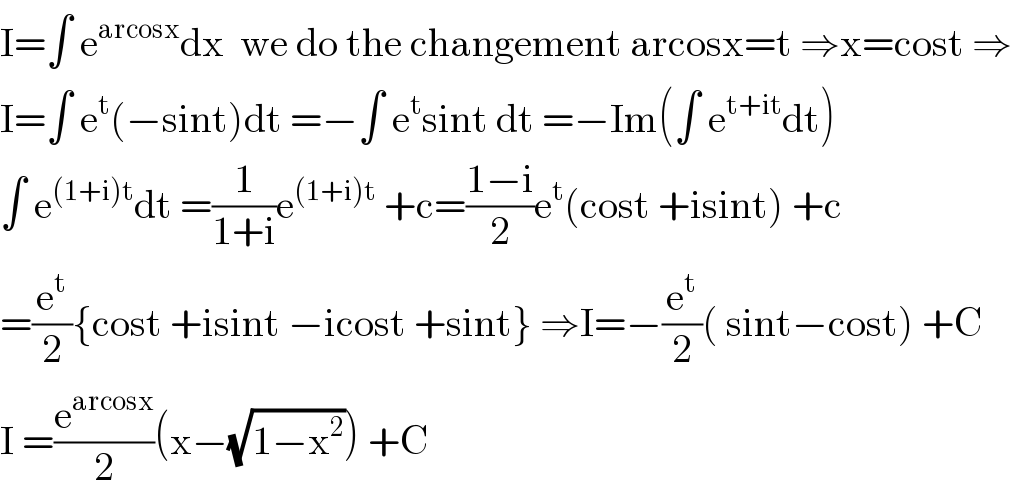
I=∫ e^(arcosx) dx we do the changement arcosx=t ⇒x=cost ⇒ I=∫ e^t (−sint)dt =−∫ e^t sint dt =−Im(∫ e^(t+it) dt) ∫ e^((1+i)t) dt =(1/(1+i))e^((1+i)t) +c=((1−i)/2)e^t (cost +isint) +c =(e^t /2){cost +isint −icost +sint} ⇒I=−(e^t /2)( sint−cost) +C I =(e^(arcosx) /2)(x−(√(1−x^2 ))) +C

$$\mathrm{I}=\int\:\mathrm{e}^{\mathrm{arcosx}} \mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{arcosx}=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{cost}\:\Rightarrow \\ $$$$\mathrm{I}=\int\:\mathrm{e}^{\mathrm{t}} \left(−\mathrm{sint}\right)\mathrm{dt}\:=−\int\:\mathrm{e}^{\mathrm{t}} \mathrm{sint}\:\mathrm{dt}\:=−\mathrm{Im}\left(\int\:\mathrm{e}^{\mathrm{t}+\mathrm{it}} \mathrm{dt}\right) \\ $$$$\int\:\mathrm{e}^{\left(\mathrm{1}+\mathrm{i}\right)\mathrm{t}} \mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{i}}\mathrm{e}^{\left(\mathrm{1}+\mathrm{i}\right)\mathrm{t}} \:+\mathrm{c}=\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\mathrm{e}^{\mathrm{t}} \left(\mathrm{cost}\:+\mathrm{isint}\right)\:+\mathrm{c} \\ $$$$=\frac{\mathrm{e}^{\mathrm{t}} }{\mathrm{2}}\left\{\mathrm{cost}\:+\mathrm{isint}\:−\mathrm{icost}\:+\mathrm{sint}\right\}\:\Rightarrow\mathrm{I}=−\frac{\mathrm{e}^{\mathrm{t}} }{\mathrm{2}}\left(\:\mathrm{sint}−\mathrm{cost}\right)\:+\mathrm{C} \\ $$$$\mathrm{I}\:=\frac{\mathrm{e}^{\mathrm{arcosx}} }{\mathrm{2}}\left(\mathrm{x}−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right)\:+\mathrm{C} \\ $$

Commented by I want to learn more last updated on 20/Dec/20

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com