
Question Number 30321 by rahul 19 last updated on 20/Feb/18
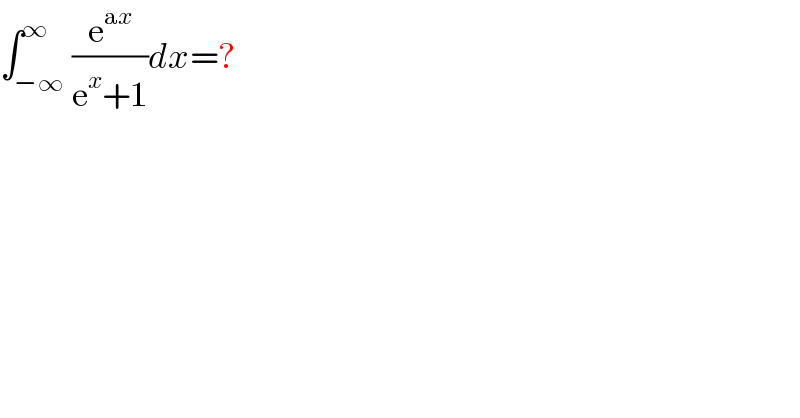
$$\int_{−\infty} ^{\infty} \frac{\mathrm{e}^{\mathrm{a}{x}} }{\mathrm{e}^{{x}} +\mathrm{1}}{dx}=? \\ $$
Commented by rahul 19 last updated on 20/Feb/18
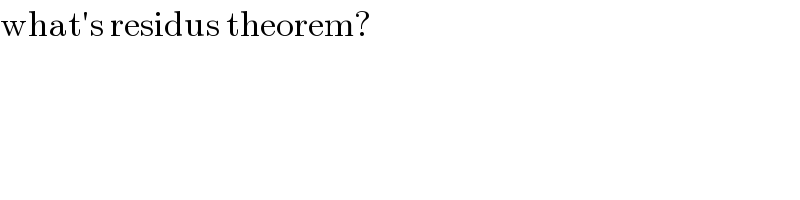
$$\mathrm{what}'\mathrm{s}\:\mathrm{residus}\:\mathrm{theorem}? \\ $$
Commented by abdo imad last updated on 20/Feb/18
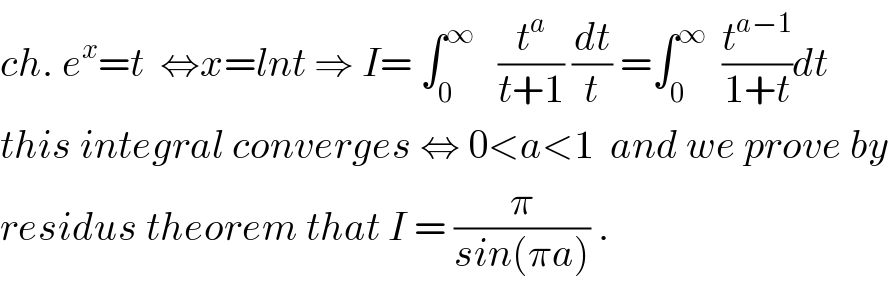
$${ch}.\:{e}^{{x}} ={t}\:\:\Leftrightarrow{x}={lnt}\:\Rightarrow\:{I}=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{{a}} }{{t}+\mathrm{1}}\:\frac{{dt}}{{t}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\: \\ $$$${this}\:{integral}\:{converges}\:\Leftrightarrow\:\mathrm{0}<{a}<\mathrm{1}\:\:{and}\:{we}\:{prove}\:{by} \\ $$$${residus}\:{theorem}\:{that}\:{I}\:=\:\frac{\pi}{{sin}\left(\pi{a}\right)}\:. \\ $$
Commented by abdo imad last updated on 20/Feb/18
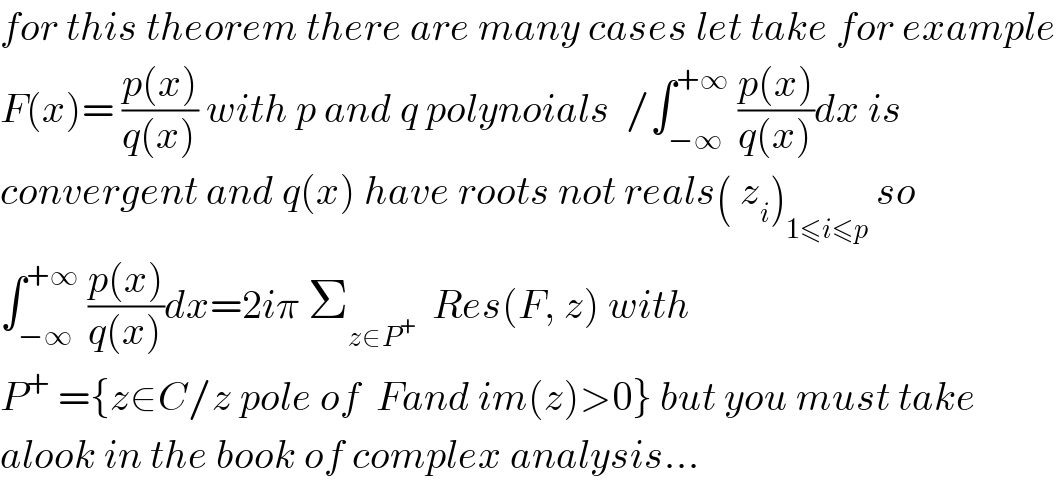
$${for}\:{this}\:{theorem}\:{there}\:{are}\:{many}\:{cases}\:{let}\:{take}\:{for}\:{example} \\ $$$${F}\left({x}\right)=\:\frac{{p}\left({x}\right)}{{q}\left({x}\right)}\:{with}\:{p}\:{and}\:{q}\:{polynoials}\:\:/\int_{−\infty} ^{+\infty} \:\frac{{p}\left({x}\right)}{{q}\left({x}\right)}{dx}\:{is} \\ $$$${convergent}\:{and}\:{q}\left({x}\right)\:{have}\:{roots}\:{not}\:{reals}\left(\:{z}_{{i}} \right)_{\mathrm{1}\leqslant{i}\leqslant{p}} \:{so} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{{p}\left({x}\right)}{{q}\left({x}\right)}{dx}=\mathrm{2}{i}\pi\:\sum_{{z}\in{P}^{+} } \:\:{Res}\left({F},\:{z}\right)\:{with} \\ $$$${P}^{+} \:=\left\{{z}\in{C}/{z}\:{pole}\:{of}\:\:{Fand}\:{im}\left({z}\right)>\mathrm{0}\right\}\:{but}\:{you}\:{must}\:{take} \\ $$$${alook}\:{in}\:{the}\:{book}\:{of}\:{complex}\:{analysis}... \\ $$
