
Question Number 128276 by john_santu last updated on 06/Jan/21
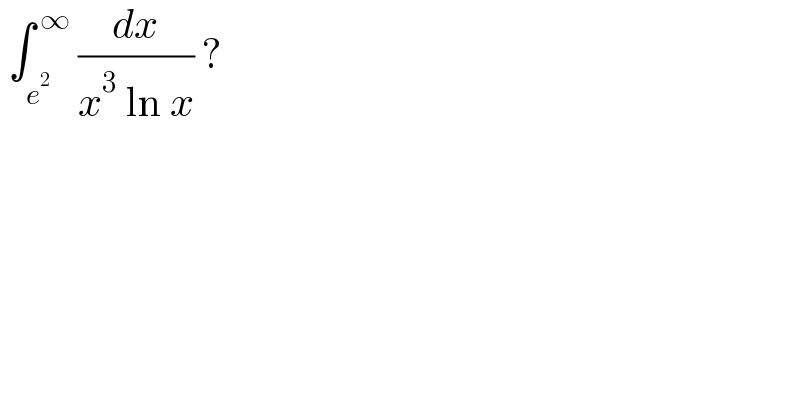
$$\:\int_{{e}^{\mathrm{2}} } ^{\:\infty} \:\frac{{dx}}{{x}^{\mathrm{3}} \:\mathrm{ln}\:{x}}\:? \\ $$
Answered by liberty last updated on 06/Jan/21
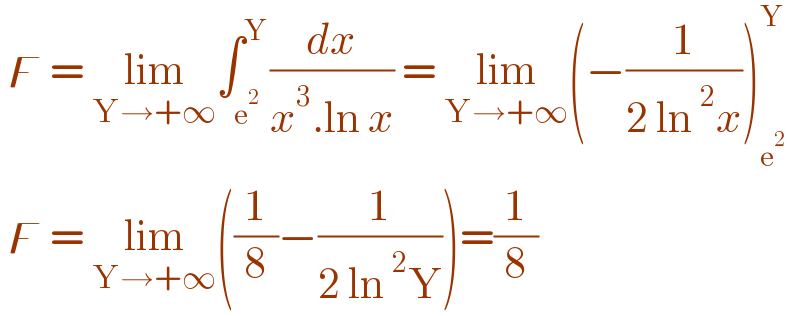
$$\:\digamma\:=\:\underset{\mathrm{Y}\rightarrow+\infty} {\mathrm{lim}}\int_{\mathrm{e}^{\mathrm{2}} } ^{\mathrm{Y}} \frac{{dx}}{{x}^{\mathrm{3}} .\mathrm{ln}\:{x}}\:=\:\underset{\mathrm{Y}\rightarrow+\infty} {\mathrm{lim}}\left(−\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{ln}\:^{\mathrm{2}} {x}}\right)_{\mathrm{e}^{\mathrm{2}} } ^{\mathrm{Y}} \\ $$$$\:\digamma\:=\:\underset{\mathrm{Y}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{ln}\:^{\mathrm{2}} \mathrm{Y}}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
