Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 47740 by tanmay.chaudhury50@gmail.com last updated on 14/Nov/18

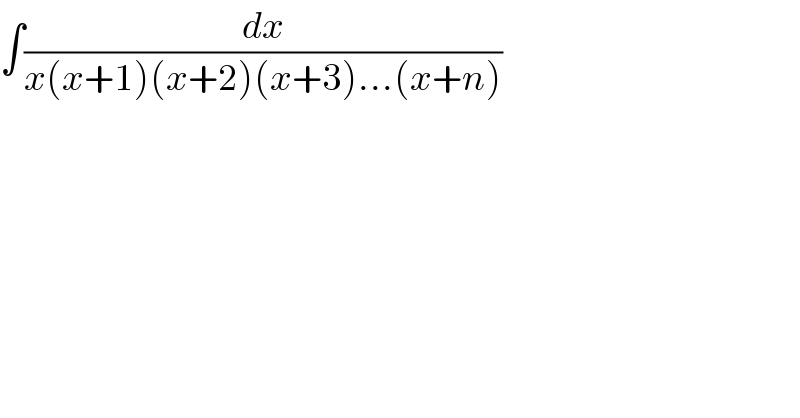
∫(dx/(x(x+1)(x+2)(x+3)...(x+n)))

$$\int\frac{{dx}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)...\left({x}+{n}\right)} \\ $$

Answered by ajfour last updated on 14/Nov/18

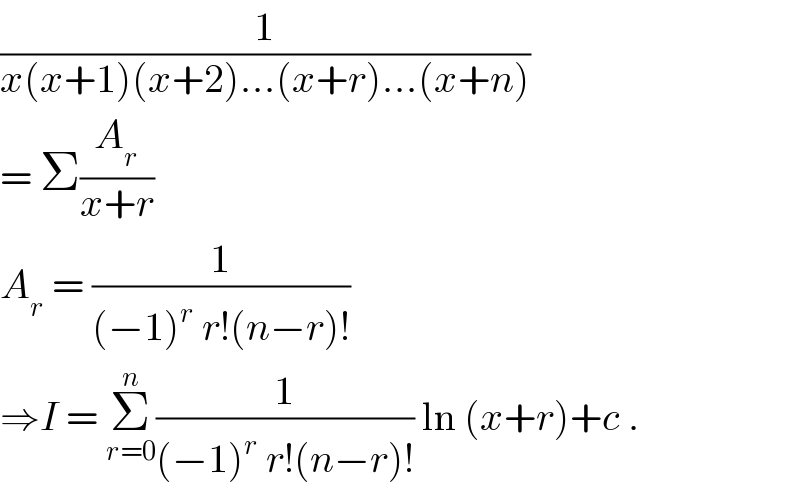
(1/(x(x+1)(x+2)...(x+r)...(x+n))) = Σ(A_r /(x+r)) A_r = (1/((−1)^r r!(n−r)!)) ⇒I = Σ_(r=0) ^n (1/((−1)^r r!(n−r)!)) ln (x+r)+c .

$$\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)...\left({x}+{r}\right)...\left({x}+{n}\right)} \\ $$$$=\:\Sigma\frac{{A}_{{r}} }{{x}+{r}}\: \\ $$$${A}_{{r}} \:=\:\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{{r}} \:{r}!\left({n}−{r}\right)!} \\ $$$$\Rightarrow{I}\:=\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{{r}} \:{r}!\left({n}−{r}\right)!}\:\mathrm{ln}\:\left({x}+{r}\right)+{c}\:. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 14/Nov/18

excellent...

$${excellent}... \\ $$

Commented by ajfour last updated on 14/Nov/18

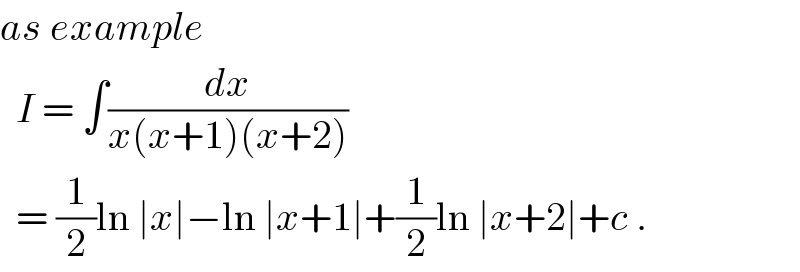
as example I = ∫(dx/(x(x+1)(x+2))) = (1/2)ln ∣x∣−ln ∣x+1∣+(1/2)ln ∣x+2∣+c .

$${as}\:{example} \\ $$$$\:\:{I}\:=\:\int\frac{{dx}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{x}\mid−\mathrm{ln}\:\mid{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{x}+\mathrm{2}\mid+{c}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 14/Nov/18

(1/(x(x+1)(x+2)(x+3)...(x+n)))=(a_0 /x)+(a_1 /(x+1))+(a_2 /(x+2))+...+(a_n /(x+n)) so 1=a_0 (x+1)(x+2)(x+3)...(x+n)+a_1 (x)(x+2)(x+3)..(x+n)+... to find a_(0 ) put x=0 a_0 ×n!=1 a_0 =(1/(n!)) similarly to find a_1 put x+1=0 a_1 (−1)(1)(2)...(n−1)=1 a_1 ×(−1)×(n−1)!=1 a_1 =(1/((−1)(n−1)!)) in this way w e find a_0 ,a_1 ,a_2 ...a_n so the intregation value is a_0 lnx+a_1 ln(x+1)+a_2 (x+2)....+a_n (x+n)+c nxt step put value of a_0 ,a_1 ,a_2 ....a_n i have solved in detail for understanding...

$$\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)...\left({x}+{n}\right)}=\frac{{a}_{\mathrm{0}} }{{x}}+\frac{{a}_{\mathrm{1}} }{{x}+\mathrm{1}}+\frac{{a}_{\mathrm{2}} }{{x}+\mathrm{2}}+...+\frac{{a}_{{n}} }{{x}+{n}} \\ $$$${so} \\ $$$$\mathrm{1}={a}_{\mathrm{0}} \left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)...\left({x}+{n}\right)+{a}_{\mathrm{1}} \left({x}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)..\left({x}+{n}\right)+... \\ $$$${to}\:{find}\:{a}_{\mathrm{0}\:} \:{put}\:{x}=\mathrm{0} \\ $$$${a}_{\mathrm{0}} ×{n}!=\mathrm{1}\:\:\:{a}_{\mathrm{0}} =\frac{\mathrm{1}}{{n}!} \\ $$$${similarly}\:{to}\:{find}\:{a}_{\mathrm{1}} \:{put}\:{x}+\mathrm{1}=\mathrm{0} \\ $$$${a}_{\mathrm{1}} \left(−\mathrm{1}\right)\left(\mathrm{1}\right)\left(\mathrm{2}\right)...\left({n}−\mathrm{1}\right)=\mathrm{1} \\ $$$${a}_{\mathrm{1}} ×\left(−\mathrm{1}\right)×\left({n}−\mathrm{1}\right)!=\mathrm{1} \\ $$$${a}_{\mathrm{1}} =\frac{\mathrm{1}}{\left(−\mathrm{1}\right)\left({n}−\mathrm{1}\right)!} \\ $$$${in}\:{this}\:{way}\:{w}\:{e}\:{find}\:{a}_{\mathrm{0}} ,{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ...{a}_{{n}} \\ $$$${so}\:{the}\:{intregation}\:{value}\:{is} \\ $$$${a}_{\mathrm{0}} {lnx}+{a}_{\mathrm{1}} {ln}\left({x}+\mathrm{1}\right)+{a}_{\mathrm{2}} \left({x}+\mathrm{2}\right)....+{a}_{{n}} \left({x}+{n}\right)+{c} \\ $$$${nxt}\:{step}\:{put}\:{value}\:{of}\:{a}_{\mathrm{0}} ,{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ....{a}_{{n}} \\ $$$${i}\:{have}\:{solved}\:{in}\:{detail}\:{for}\:{understanding}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com